Models for simplification of antenna calculations
boundaries
model
Figure 1: Models for simplification of antenna calculations

boundaries
model
Figure 1: Models for simplification of antenna calculations.
Models for simplification of antenna calculations
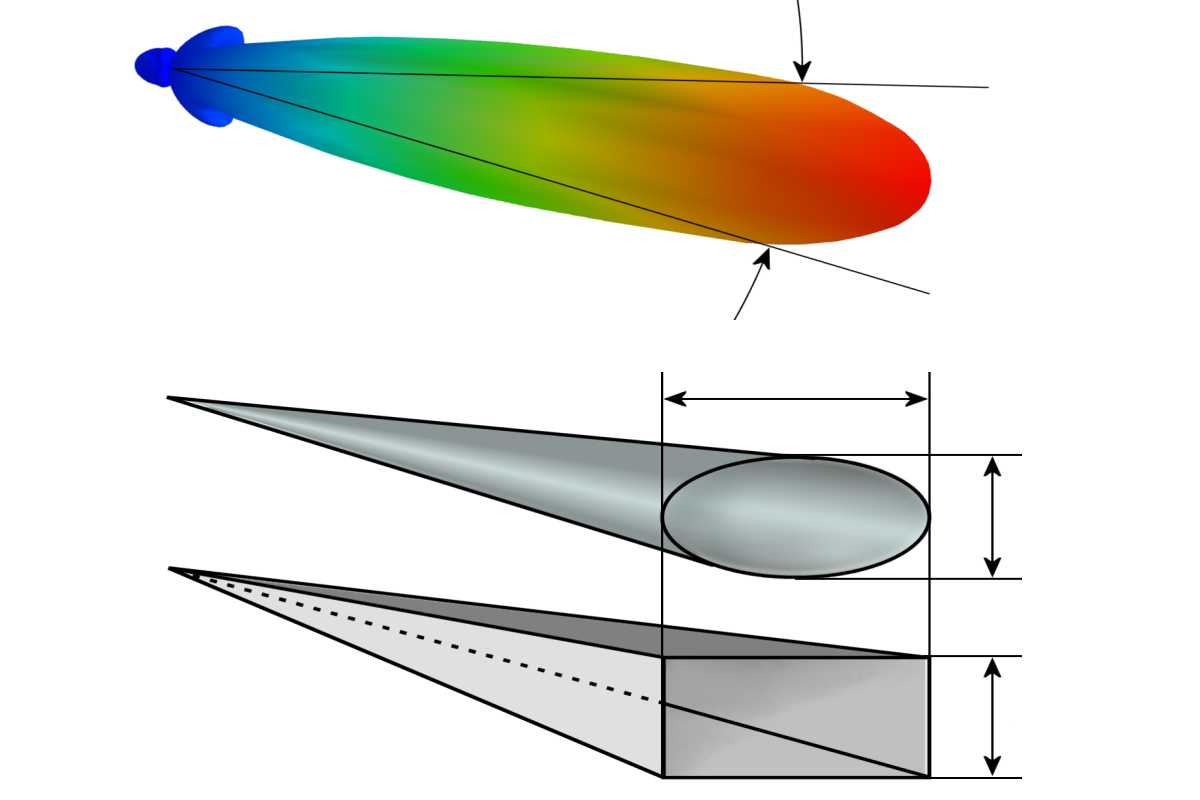
The radiation of any real antenna follows rather complicated rules. The radiated energy varies depending on angular deviations and losses due to side lobes occur. To be able to calculate for example directivity and antenna gain, some simplifications for the antenna calculation or models are agreed upon, which can be used for a mathematical consideration with sufficient approximation.
As simplifications are assumed
- that the radiated energy is completely concentrated in the main lobe of the antenna pattern. There would be no side lobes.
- All radiated energy is within the half-width of the antenna – outside these −3 dB boundaries, there is no energy radiation.
- Within the −3 dB boundaries, the energy is uniformly distributed.
Applying these assumptions separately to the vertical and horizontal half-power beam widths of the antenna results in a rectangular model (see Figure 1, below). When these angles are combined to form a solid angle, the result is a model with an elliptical shape of the antenna pattern (see Figure 1, middle).
Application of the rectangular model
When calculating an antenna gain, the energy radiated directionally by the antenna is compared with that of an isotropic antenna. The isotropic antenna distributes the transmitted energy uniformly over a spherical surface. Let the area irradiated by the directional antenna be rectangular with lengths of a and b.
| a = r sinφ | |
| b = r sinθ | (1) |
with half-power beam widths φ for the azimuth angle and θ for the elevation angle, both in radians. Thus, the area is
| ab = r² sinφ sinθ | (2) |
The antenna gain is thus:
| G = | spherical surface area | = | 4π r² | = | 4π | (3) |
| rectangle area | r² sinφ sinθ | sinφ sinθ |
The inaccuracy that the rectangular area considered here is actually a rectangular section of a spherical surface in real terms can be completely neglected in the case of strong directivity, i.e., small angles. By the model-like consideration already much larger inaccuracies were accepted.

Figure 2: Comparison of the models with the real measured result using the example of a symmetrical parabolic antenna (φ = θ)
Application of the elliptical model
Analogous to the calculation above, we now need to calculate the area of the ellipse. For this we use the equation with the semi-axes a and b, which are now both but only half as large as the side lengths of the rectangle above.
| A = π ab = π[(r sinφ)/2][r sinθ)/2] = (πr²sinφ sinθ)/4 | (4) |
Since the area of the ellipse is visibly smaller than the rectangle, there must therefore be a slightly larger antenna gain here.
| G = | sphere surface area | = 4π r² | 4 | = | 16 | (5) |
| elliptical area | πr²sinφ sinθ | sinφ sinθ |

values
Figure 2: Comparison of the models with the real measured result using the example of a symmetrical parabolic antenna (φ = θ)
The difference between both models is practically the difference between 16 and 4π and is about 78%. The correction of these inaccuracies is done by a so-called antenna efficiency factor ka, which is estimated for each antenna shape. However, it must always be taken into account for which antenna model this efficiency factor applies. The diagram in Fig. 2 compares the results of the model calculations with the real measured values of symmetrical parabolic antennas. Compared to the elliptical model, the antennas have an efficiency factor of ka = 0.47 . The rectangular model has an efficiency factor of ka = 0.6 .
