Modelle für die Vereinfachung von Antennenberechnungen
Grenzen
Modell
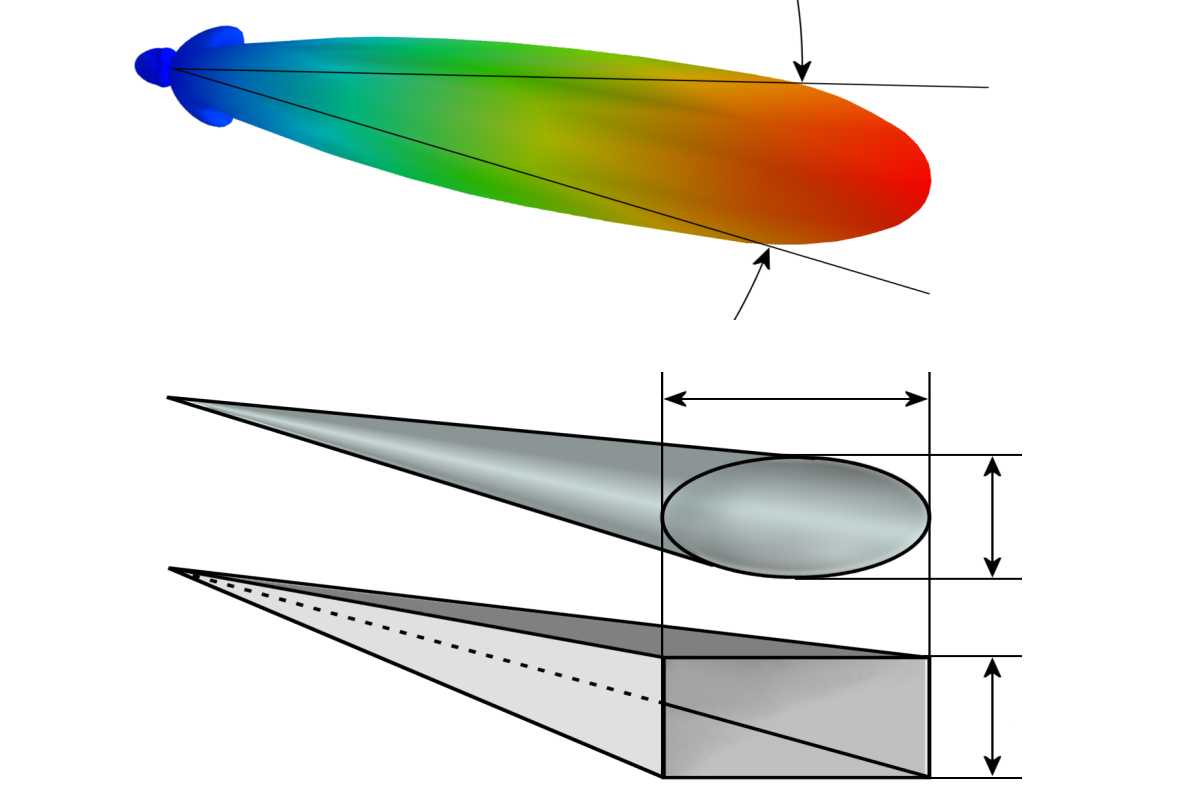
Bild 1: Modelle für die Vereinfachung von Antennenberechnungen

Grenzen
Modell
Bild 1: Modelle für die Vereinfachung von Antennenberechnungen
Modelle für die Vereinfachung von Antennenberechnungen
Die Abstrahlungen einer beliebigen realen Antenne erfolgen nach recht komplizierten Regeln. Die abgestrahlte Energie variiert abhängig von Winkelabweichungen und es treten Verluste durch Nebenkeulen auf. Um eine Berechnung von zum Beispiel Richtwirkung und Antennengewinn vornehmen zu können, werden einige Vereinfachungen für die Antennenberechnung oder auch Modelle vereinbart, die zu einer mathematischen Betrachtung mit ausreichender Näherung genutzt werden können.
Als Vereinfachungen werden angenommen:[1]
- dass die abgestrahlte Energie vollständig in der Hauptkeule des Antennendiagramms konzentriert sei. Es gäbe also keinerlei Nebenkeulen.
- Alle abgestrahlte Energie befinde sich innerhalb der Halbwertsbreite der Antenne – außerhalb dieser −3 dB Grenzen sei keine Energieabstrahlung.
- Innerhalb der −3 dB Grenzen sei die Energie gleichmäßig verteilt.
Wenn diese Annahmen auf die vertikale und die horizontale Halbwertsbreite der Antenne getrennt angewendet werden, führt das zu einem rechteckigen Modell (siehe Bild 1, unten). Wenn diese Winkel zu einem Raumwinkel einer Ellipse verknüpft werden, dann entsteht ein Modell mit einer elliptischen Form des Antennendiagramms (siehe Bild 1, mitte).
Anwendung des rechteckigen Modells
Bei der Berechnung eines Antennengewinns wird die von der Antenne gerichtet abgestrahlte Energie mit der einer isotropen Antenne verglichen. Die isotrope Antenne verteilt die Sendeenergie gleichmäßig auf eine Kugeloberfläche. Die von der Richtantenne bestrahlte Fläche sei rechteckig mit den Kantenlängen a und b.
| a = r sinφ | |
| b = r sinθ | (1) |
mit den Halbwertsbreiten φ für den Seitenwinkel und θ für den Höhenwinkel, beide in Radiant. Die Fläche ist also
| ab = r² sinφ sinθ | (2) |
Der Antennengewinn ist somit:
| G = | Kugeloberfläche | = | 4π r² | = | 4π | (3) |
| Rechteck | r² sinφ sinθ | sinφ sinθ |
Die Ungenauigkeit, dass die hier betrachtete rechteckige Fläche real eigentlich ein rechteckiger Ausschnitt aus einer Kugeloberfläche ist, kann bei starker Richtwirkung, also bei kleinen Winkeln, völlig vernachlässigt werden. Durch die modellhafte Betrachtung wurden schon sehr viel größere Ungenauigkeiten in Kauf genommen.

Bild 2: Vergleich der Modelle mit dem realen Messergebnis am Beispiel einer symmetrischen Parabolantenne (φ = θ)
Anwendung des elliptischen Modells
Analog zur obigen Berechnung müssen wir jetzt die Fläche der Ellipse berechnen. Hierfür nutzen wir die Gleichung mit den Halbachsen a und b, die jetzt beide aber nur halb so groß sind, wie die Seitenlängen des obigen Rechteckes.
| A = π ab = π[(r sinφ)/2][r sinθ)/2] = (πr²sinφ sinθ)/4 | (4) |
Da die Fläche der Ellipse sichtlich kleiner ist als das Rechteck muss hier also ein etwas größerer Antennengewinn entstehen.
| G = | Kugeloberfläche | = 4π r² | 4 | = | 16 | (5) |
| Ellipsenfläche | πr²sinφ sinθ | sinφ sinθ |

Bild 2: Vergleich der Modelle mit dem realen Messergebnis am Beispiel einer symmetrischen Parabolantenne (φ = θ)
Der Unterschied zwischen den Modellen ist praktisch die Differenz zwischen 16 und 4π und liegt bei etwa 78%. Die Korrektur dieser Ungenauigkeiten erfolgt über einen sogenannten Antennen-Effizienzfaktor ka, der für jede Antennenform individuell abgeschätzt wird. Hierbei muss aber immer beachtet werden, für welches Antennenmodell dieser Effizienzfaktor gilt. Das Diagramm in Bild 2 vergleicht die Ergebnisse der Modellrechnungen mit den real gemessenen Werten von symmetrischen Parabolantennen. Gegenüber dem elliptischen Modell haben die Antennen einen Effizienzfaktor von ka = 0,47. Das rechteckige Modell kommt dabei auf einen Effizienzfaktor von ka = 0,6.
In der Radartechnik werden diese Vereinfachungen vor allem dort verwendet, wo es nur um eine qualitative Bewertung geht, zum Beispiel eine Positionsbestimmung oder ein Winkelauflösungsvermögen. Auch die statistischen Fluktuationsmodelle von P. Swerling verwenden das rechteckige Antennenmodell. Sobald jedoch die Größe des Echosignals bewertet werden soll (zum Beispiel bei Reichweiteberechnungen), kann diese Vereinfachung nur dann vorgenommen werden, wenn die bereits in der Radargrundgleichung genannten Verlustgrößen mit einberechnet werden.
Source:
- NAVAIR Electronic Warfare/Combat Systems: ’’Electronic Warfare and Radar Systems Engineering Handbook’’, 1 Jun 2012, p. 64 (PDF) p. 3-1.2 (Print) (online)
