Yönlülük ve Anten Kazancı
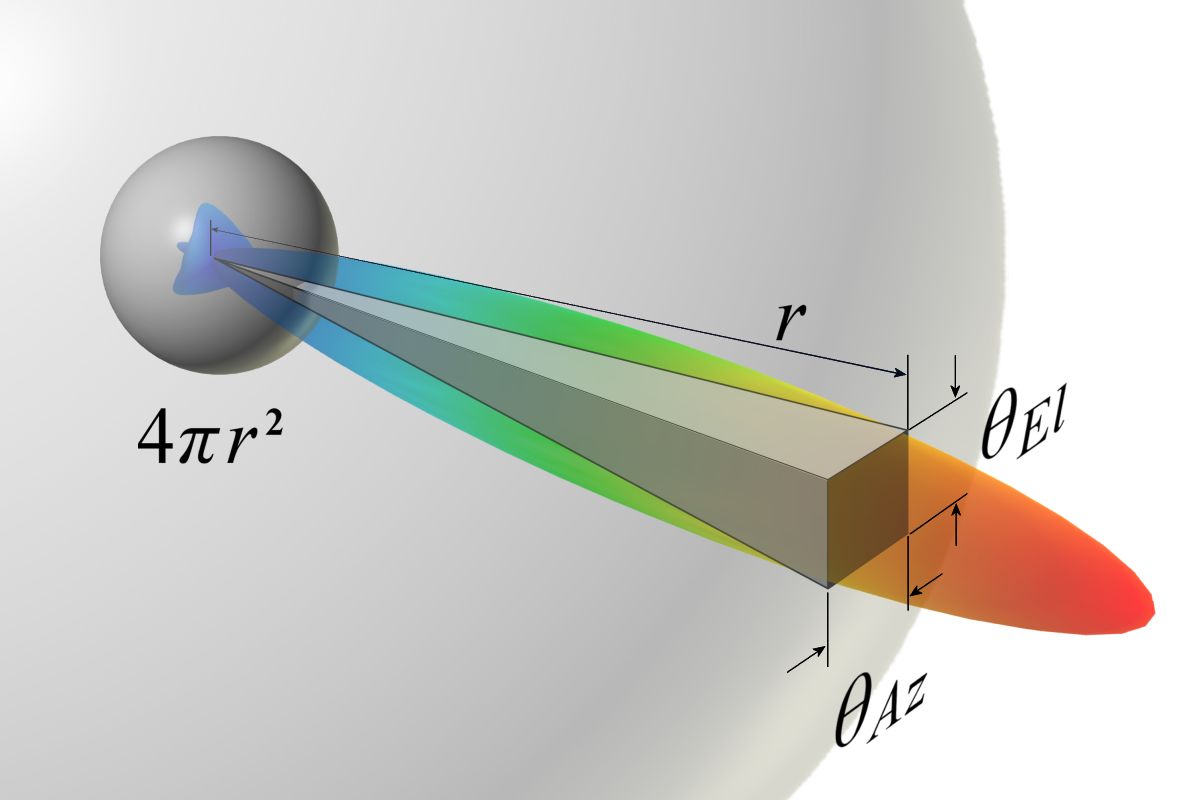
Resim 1: Yönlü antenin ışıma yüzeyinin bir küre yüzeyi ile karşılaştırılması
(Dikkat: Karşılaştırma sırasında kürenin yarıçapı dikdörtgenin merkez noktadan olan uzaklığına eşit olmalıdır.)

Resim 1: Yönlü antenin ışıma yüzeyinin bir küre yüzeyi ile karşılaştırılması
(Dikkat: Karşılaştırma sırasında kürenin yarıçapı dikdörtgenin merkez noktadan olan uzaklığına eşit olmalıdır.)
Yönlülük ve Anten Kazancı
G anten kazancı, bir antenin D Yönlülüğünü ve η verimliliğini tanımlamakta kullanılan bir basit parametredir.
Bir antenin yönlülüğü
Bir antenin yönlülüğü, bir gerçek antenin ana ışıma yönündeki S Güç Yoğunluğunun (birim alana düşen ışıma gücü), tüm yönlere eşit yayın yapan bir varsayımsal (hypothetical), gerçekte var olmayan, bir yönbağımsız ışıyıcının (isotropic radiator) ışıma yoğunluğuna olan oranıdır. Yönbağımsız ışıyıcının güç yoğunluğu bu nedenle bir küresel yüzeye eşit biçimde dağılmış olan güçtür. Her gerçek antenin az ya da çok bir belirgin yönlülüğü vardır. Yönlülük, gerçek antenin ana ışıma yönündeki güç yoğunluğunun yönbağımsız ışıyıcının aynı yöndeki güç yoğunluğuna olan oranı olarak tanımlanır:
| D = | S |
S = Gerçek antenin güç yoğunluğu Si = Yön bağımsız antenin güç yoğunluğu |
(1) | |
| Si |
Yönlü bir anten ışıma gücünü küresel yüzeyin yalnızca bir küçük bölümüne yoğunlaştırır. Bu yüzey parçası ile tüm küre yüzeyi arasında bir ilişki de kurulabilir. Bu yüzey kesri (fraction), iki yarı-güç demet genişliği (half-power beam-width) ile radyan cinsinden hesaplanır. (Bu radyan ölçütünde, birim dairenin yarıçapı da hesaba katılır ve kürenin yüzeyinin yarıçapı bu değer kadar kısaltılır.) Bu etkili alanın yüksekliği ve genişliği kullanılan dalga boyunun bir katı olarak tanımlanır.
| D = | AKüre | ≅ | 4π r2 | = | 4π | = | 4π · AEtkin |
AKüre = Yarıçapı = 1 olan bir kürenin toplam yüzeyi AEtkin = b·h = Küre yüzeyindeki etkin yüzey θAzi = Azimut açısında Yarı Güç Genişliği (radyan cinsinden) θYük = Yükseklik açısında yarı güç genişliği (radyan cinsinden) b = Yüzey genişliği h = Yüzey yüksekliği |
(2) | |
| AEtkin | θAzi · θYük | λ/b · λ/h | λ2 |
(Ancak burada, AEtkin = b·h yüzeyinin küre yüzeyinde değil, bir düzlemde olması nedeniyle bir belirsizlik söz konusudur. b·h yüzeyi, küre yüzeyine göre ne kadar küçükse bu belirsizlik o kadar az, antenin yönlülüğü de o kadar iyi olur. 20° ye kadar olan açıklık açılarında bu belirsizlik ihmal edilebilir.)
Bir antenin anten kazancı
Yönlülük bir anten kazancının önemli bir bileşenidir. Bir gerçek antenin kazancında kazançlar ve kayıplar dikkate alınmalıdır. Bir antenin ışıma gücü, her bir anten için antene giden besleme hatlarında oldukça kolay ölçülebilen besleme gücüne doğru orantılıdır. Ancak bu besleme gücünün bir bölümü antene giden hatların omik dirençlerinde kaybolur. Bu kayıplar bir antenin verimliliğini belirler. Bu kayıpların olmadığı bir ideal antende antenin kazancı yönlülüğüne eşit olurdu.
Anten kazancı, yönlülükten verimlilik katsayısı kadar daha azdır.
| G = η· D | (3) |
Anten kazancı her zaman 1 den büyük olmamalıdır. Anten kazancı 1 den daha küçük olan antenlerde vardır. Bunlar genellikle farklı frekans bantlarında elde edilen ölçüm sonuçlarını karşılaştırmanın önemli olduğu, anten kazancının çok büyük bir frekans bölgesinde düzgün büyüklükte dağıldığı ölçüm antenleridir.
Basitleştirmeler
Küresel bir ışıyıcının küresel yüzeyini ve bir antenin etkili yüzeyini birbiriyle ilişkilendirebilmek için bazı basitleştirmeler yapılmalıdır:
- Yayılan enerjinin tamamının antenin ana topuzunda (main lobe) olduğu, yani, hiçbir yan topuz (side lobe) bulunmadığı varsayılır.
- Yayılan enerjinin tamamının antenin ölçülen yarı güç genişliği içinde yoğunlaştığı varsayılmaktadır. Yani: bu yarı güç genişliğinin dışında herhangi bir güç bulunmamaktadır.
- Yarı güç genişliği içinde enerjinin düzgün dağıldığı kabul edilir. (Böylece bir koni biçimli şekilden, dikdörtgen tabanı yükseklik açısında yarı güç genişliği ve azimut açısında yarı güç genişliği olan bir piramit meydana gelir!)
Yalnızca bu varsayılan basitleştirmeler sayesinde, iki geometrik yüzey (küre ve dikdörtgen) birbiriyle karşılaştırılabilir.
