Koordinatenbestimmung
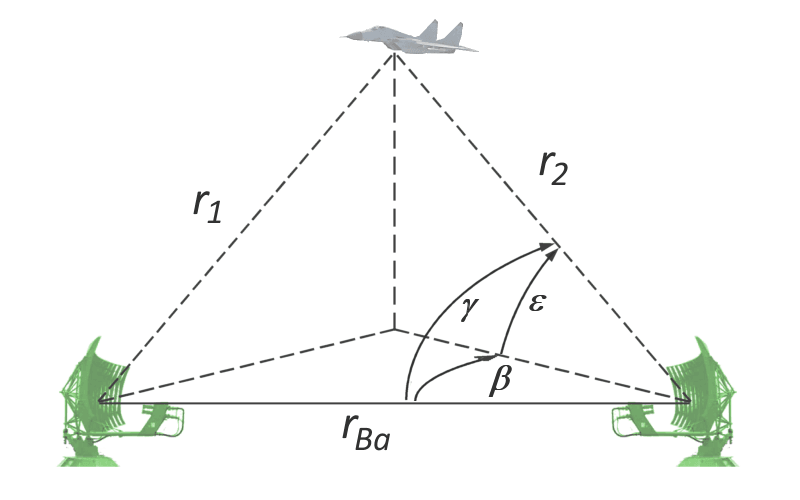
Bild 1: Koordinatenbestimmung mit einem Bistatischen Radar
Koordinatenbestimmung
Der Sendeimpuls gelangt auf zwei Wegen zum Empfänger: auf dem direkten Weg und nach der Reflektion am Ziel. Dabei wird die gesamte Entfernung rΣ = r1 + r2 gemessen und der Seitenwinkel β und der Höhenwinkel ε des empfangenen Signals bestimmt.
Die für die Messung der Entfernung rΣ notwendige Information über den Beginn der Zeitmessung kann auf dem Wege des direkten Empfangs des Sendeimpulses bei genau bekannter Entfernung rBa (Basis des zu betrachtenden Dreiecks) erhalten werden.
Die Entfernung rΣ bestimmt die Lage des Zieles auf der Oberfläche eines Rotationsellipsoides, in dessen Brennpunkten die Sende- und die Empfangsantenne stehen.
Das Ziel liegt im Schnittpunkt der Oberfläche dieses Rotationsellipsoides mit der Geraden, die die Richtung charakterisiert, aus der das reflektierte Signal eintrifft. Die Entfernung des Zieles von der Empfängerantenne r2 kann mit Hilfe des Kosinussatzes und der gemessenen Gesamtentfernung rΣ ermittelt werden:
.print.png)
.png)
(1)
Dieses Gleichungssystem mit den zwei Unbekannten kann zur folgenden Gleichung umgeformt werden:
.print.png)
.png)
(2)
Die Größe des Winkels γ wird aus den gemessenen Winkeln β und ε auf der Grundlage der Beziehung zwischen diesen drei Winkeln bestimmt:
.print.png)
(3)
Bei einem nur zweidimensional messenden Radar ist γ = β.

Bild 2: Messprinzip des passiven Radars Klein Heidelberg Parasit
Eine der ersten Nutzungen dieses Prinzips geschah im 2. Weltkrieg durch das passive Radar Klein Heidelberg Parasit. Dieses Radar verwendete die Abstrahlungen der Sender des britischen Chain Home . Die verschiedenen Sendetürme der Chain Home arbeiteten nach einem bestimmten Zeitplan. So konnte mit einem Zeitschalter und einer Torschaltung einer der Sender ausgewählt werden.
Durch Messung der Verzögerungszeit zwischen direkt empfangenem Signal und dem reflektierten Signal wurde die Entfernungsdifferenz bestimmt. Wegen der Mehrdeutigkeit im Gleichungssystem mit zwei Gleichungen und drei Unbekannten, ergibt die Verzögerungszeit alle möglichen Orte, die dann eine Ellipse mit Sender und Empfänger in den Brennpunkten bilden.
Die Empfangsantenne konnte jedoch gedreht werden und mit ihrem Antennendiagramm den Winkel β als dritte Variable bestimmen. Somit wurde das Messergebnis eindeutig. Die Genauigkeit konnte verbessert werden, indem zur Peilung die erste Nullstelle des Antennendiagramms verwendet wurde.


