Multilateration
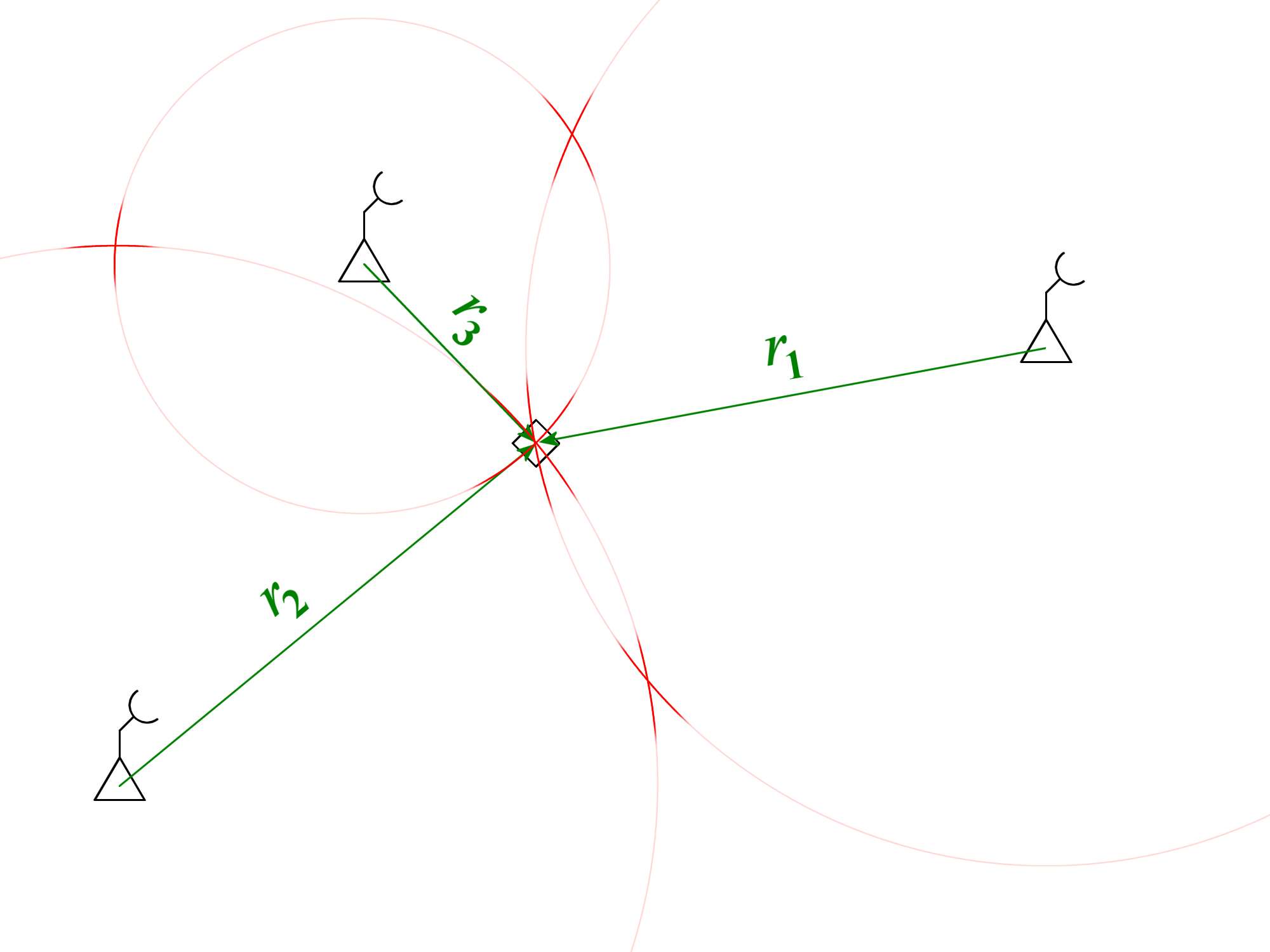
Figure 1: The operation of the multilateration
(here the special case of trilateration: three distances to three known points determine a new position)

Figure 1: The operation of the multilateration
(here the special case of trilateration: three distances to three known points determine a new position)
Multilateration
Multilateration is the process of determining locations of points by measurement of distances from known points. In Air Traffic Management the measurement of distances is performed by various radar methods by devices installed at these known points. In contrast to triangulation, it does not involve the measurement of angles. That’s why big directional antennas are not necessary.
Functionality
Time-synchronous Measurements
The object to be measured is irradiated (primary radar method) or emits a signal on request (secondary radar method). This echo or response signal is received by a fixed receiver using an omni-directional antenna. The runtime is a measure of the distance. Since a direction determination is not yet possible, the object to be measured is located somewhere around the receiver on a circular line with the radius of the measured distance.
The same process using a second receiver gives a second circle around its fixed position. The object to be measured must be located on one of the two intersections of these circles. This result is still ambiguous. The third receiver from a third fixed position gives an unambiguous result because three circles can only have one common point of intersection.
Synchronicity is established by the time of the transmitted interrogation (or the radar pulse). If each receiver transmits the interrogation itself, the ranging is simple like a monostatic radar. It is an equation with only one unknown quantity, that can be easily calculated. If only one central transmitter emits the interrogation, the distance measurement becomes a bit more complicated like with a bistatic radar. There are now two unknown quantities in the calculation: The distance from the transmitter to the object (which is constant for each receiver) and the distance from the object to the respective receiver.

Figure 2: Non-synchronous multilateration, also-called hyperbolic navigation
Non-synchronous Multilateration
There is also the possibility that the object to be measured regularly transmits a broadcasting message without any interrogation (example given: ADS-B). Here the exact transmission time is unknown. The receivers only recognize the exact arrival time of the transmission signal. It is therefore not possible to measure the runtime between the object and a single receiver, but only the runtime difference in comparison between the leading edge of the signals in two receivers on different sites. (The transit times in the cable connections between the receivers and the server are calibrated and can be deducted.)
Between two receivers, the different runtime differences are represented as a group of hyperbolas. Each hyperbola in this group corresponds to exactly one measured runtime difference. This means that at this given runtime difference, the object to be measured may be somewhere on this hyperbola.
Further pairs of receivers also measure a difference in runtime and also get a dedicated hyperbola from their individual group of hyperbolas. The intersection of all these selected hyperbolas is the position you are looking for.
Technical Realization
Multiple frequency ranges may be used for an application of multilateration to detect moving obstacles at aerodromes. For this purpose, there is a similar transponder in every vehicle on the airfield, as prescribed in airplanes. To alleviate congestion on the 1090 MHz band, the Federal Aviation Administration (FAA) created another option for ADS-B solutions that run on a dedicated 978 MHz band – Universal Access Transceiver, or UAT. 978 UAT radios can be configured to provide both ADS-B “Out” and “In” capability in a single product. The ADS-B “Out” broadcast on 978 MHz carries all the same tracking data sent by Extended Squitter (ES) transponders on 1090 MHz. However, on the ADS-B “In” side, the additional bandwidth afforded by the 978 MHz spectrum allows for a much more extensive list of data uplink services. The ADS-B system provides aircraft/vehicle position information using data provided by the unit’s GPS navigation system and transmitted via Mode S Extended Squitter (1090 MHz) or Universal Access Transceiver (978 MHz). Airport authorities or entities approved by the FAA can apply to operate up to 200 vehicle squitters under a single application.[1]
The location information of the vehicle now has two independent sources: once the GPS integrated with the transponder and additionally the multilateration. In order to alleviate congestion the heavily used response frequency of the secondary radar (1090 MHz), the GPS shuts down the ADS-B when the vehicle is not on taxiways or the runway.
Measurement Errors
By a very large number of such receivers on the airfield measuring errors can be statistically suppressed. Measuring errors occur especially when strong noise or active interference falsify the measurement of the leading edge of the received signal. Furthermore, multiple reflections can affect the measurement of the runtime. The probability of such measurement errors decreases with the reduction of the distance to be measured. Therefore only measurement results from the near range are used for the location determination.
Sources and ressources:
- ICAO: Airport Ground Vehicle Automatic Dependent Surveillance – Broadcast (ADS-B) Out Squitter Equipment — 11/14/2011, (online)

