Rayleigh- en Mie-verstrooiing
gebied
gebied
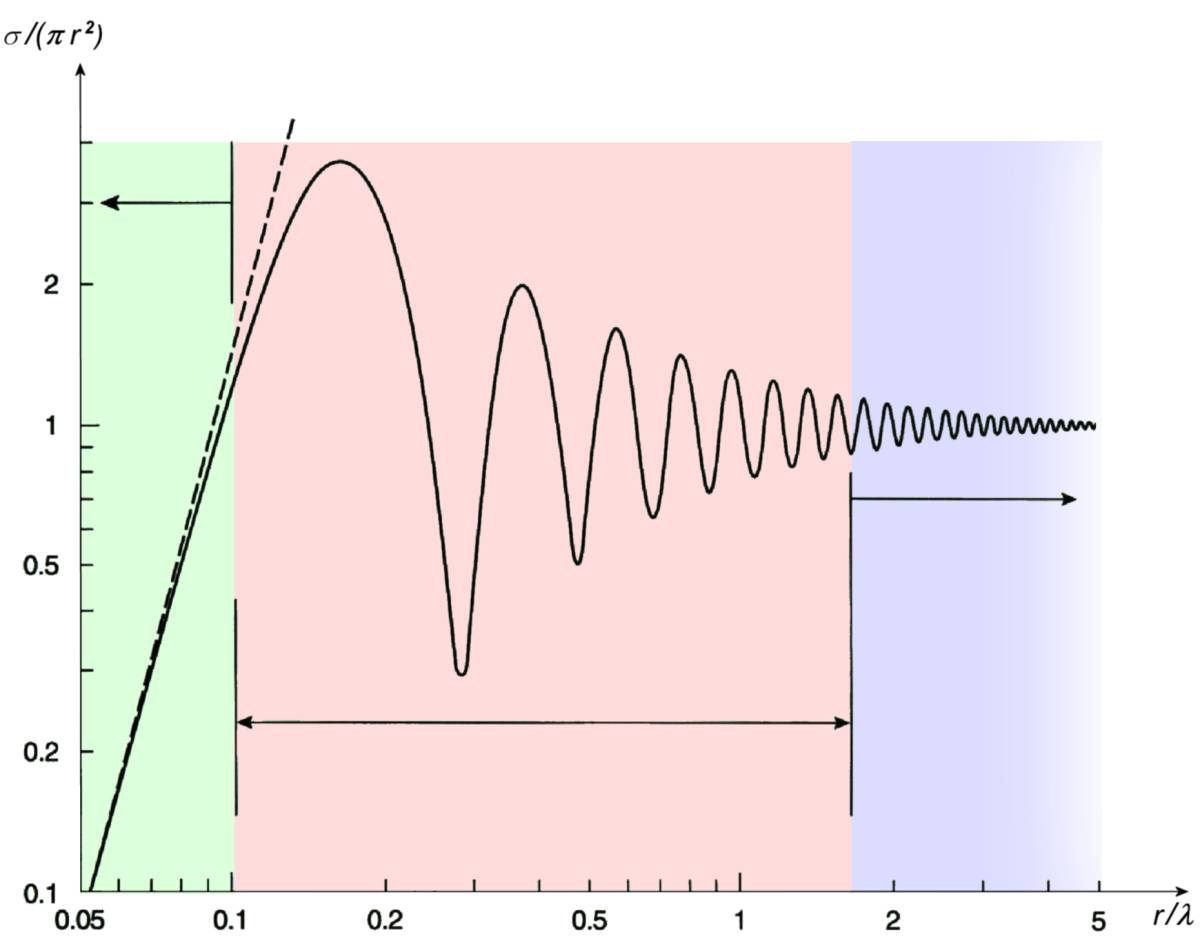
Figuur 1: Rayleigh- en Mie-verstrooiing, en optisch gebied

gebied
gebied
Figuur 1: Rayleigh- en Mie-verstrooiing, en optisch gebied
Rayleigh- en Mie-verstrooiing
Figuur 1 toont de verschillende gebieden die van toepassing zijn op de berekening van de radardoorsnede van een sfeer. De regels van het optische gebied ("verre veld" tegenhanger) zijn van toepassing wanneer (2π·r/λ);>10. In dit gebied is de radardoorsnede van een sfeer onafhankelijk van de frequentie. Het reflecterend oppervlak van de sfeer is hier gelijk aan het oppervlak van een cirkel met de straal van de sfeer
(1)
De vergelijking van de radardoorsnede gaat vooral stuk door kruipende golven in het gebied waar 2π · r. De grootste positieve verstoring van de radardoorsnede (punt A) zou 4 maal groter zijn dan de radardoorsnede berekend met de formule van het optisch gebied. Er treedt net een minimum op (punt B) en de werkelijke radardwarsdoorsnede zou 0,26 maal zo groot zijn als de waarde die met de formule van het optische gebied is berekend. Dit gebied staat bekend als het „Mie” of „resonantiegebied”..
Als we een sfeer met een diameter van één meter zouden gebruiken, zouden de interferenties optreden bij 95 MHz, zodat elke frequentie boven 950 MHz voorspelde resultaten zou geven.
De grootte van het sfeervormige reflectiegebied is kleiner dan de golflengte in het gebied van de „Rayleigh-verstrooiing”. De radardoorsnede wordt hier berekend met de formule
(2)
De „Rayleigh-Scattering” is een typisch toepassingsgeval voor weerradars.
Bij benadering is dit lager L-Band houdt nog rekening met de Mie-verstrooiing bij luchtverdedigings- en luchtverkeersleidingsradar. Bij frequenties boven 1 GHz zijn er overwegend optische omstandigheden.
Kwalitatieve afleiding

Figuur 2: Tijdvertraging van de circulerende golf ten opzichte van de direct gereflecteerde golf.
De in de interferentie aanwezige energiecomponenten zijn enerzijds de direct in het middelpunt van de sfeer gereflecteerde energie, die echter tijdens de reflectie een fasesprong van 180° ondergaat. Het tweede deel is het resultaat van een kruipende golf, die wordt opgewekt door een voortdurende diffractie aan het oppervlak van de sfeer. Deze kruipende golf moet een omweg nemen, afhankelijk van de diameter van de sfeer. Beide componenten overlappen elkaar in fase in de lokale maxima van het diagram in figuur 1 en in fase-tegenstelling in de lokale minima.
Indien voor de vereenvoudiging wordt aangenomen dat de circulatiegolf direct op het oppervlak van de sfeer loopt, kan de omweg volgens fig. 2 worden berekend uit de som van de diameter en de halve omtrek van de cirkel (sferische doorsnede). Het eerste minimum treedt dus op zijn vroegst op wanneer de omweg gelijk is aan de halve golflengte en de faseverschuiving ten gevolge van de tijdvertraging van de omweg (zoals de fasesprong bij reflectie) ook 180° is. Alle verdere lokale maxima en minima treden op bij een grootte van de omweg die gelijk is aan zowel het even als het oneven veelvoud van de halve golflengte.
Aangezien er een kleine afstand is tussen het oppervlak van de sfeer en het pad van de circulerende golf, kan de benadering 2πr worden gebruikt in plaats van (2+π)r.
De verouderde Russische VHF -radars werkten bijvoorbeeld op frequenties tussen 145 en 175 MHz, wat overeenkomt met een golflengte van 1,7 tot 2,1 meter. Voor de geometrische afmetingen van een jachtvliegtuig (ongeveer 2,5 tot 4 m omtrek van de romp) komt dit overeen met een positie in het afgebeelde diagram ongeveer het tweede maximum (boven de letter B).

