Doppler Dilemma
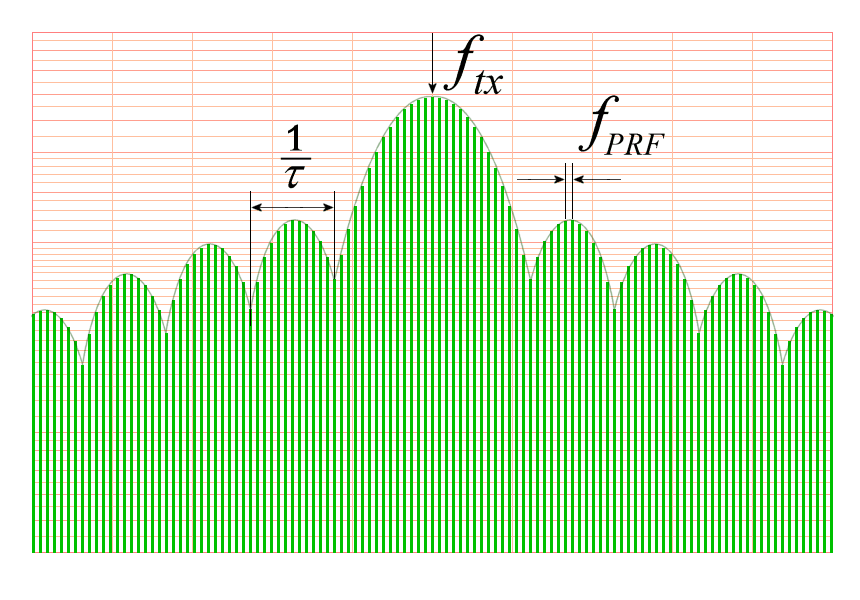
Figuur 1: Weergave van een radarsignaal op een spectrumanalysator
Doppler Dilemma
Bij een pulsradar bestaat de modulatie van de uitzendfrequentie uit een periodieke opeenvolging van vierkante pulsen. Het frequentiespectrum van dit uitgezonden signaal is een kamvormig lijnenspectrum met een lijnafstand die gelijk is aan de pulsherhalingsfrequentie. De afzonderlijke lijnen kunnen niet worden gescheiden door een vergelijking van de amplitude. Bij een bewegende reflector wordt het gehele lijnenspectrum van het ontvangen signaal in Figuur 1 door het dopplereffect enigszins naar links of naar rechts verschoven, afhankelijk van de richting van de radiale snelheid. Een ontvangen spectrum dat door het dopplereffect is verschoven, kan alleen voor een ondubbelzinnige snelheidsmeting worden gebruikt als de verschuiving van het gehele spectrum kleiner is dan de lijnafstand in het spectrum. Dit betekent dat de Doppler-frequentie kleiner moet zijn dan de pulsherhalingsfrequentie fPRF.
Met behulp van de vergelijking voor de Doppler-frequentie fD kan het bereik van de unieke radiale snelheid vr worden berekend:
| fPRF > |fD| = | 2 · vr · ftx | (1) |
| c0 |
| vr < | c0 · fPRF | (2) |
| 2 ftx |
Deze vergelijking is alleen van toepassing indien de verplaatsingsrichting bekend is, d.w.z. indien bekend is of het doel zich van de radar verwijdert of ernaar toe beweegt. Is dit niet bekend, dan wordt de unieke waarde van de snelheid weer gehalveerd:
| vr < | c0 · fPRF | (3) |
| 4 ftx |

Figuur 2: Frequentie-afhankelijkheid van een ondubbelzinnige meting van de maximale afstand en de maximale radiale snelheid

Figuur 2: Frequentie-afhankelijkheid van een ondubbelzinnige meting van de maximale afstand en de maximale radiale snelheid
De pulsherhalingsfrequentie bepaalt echter ook de ondubbelzinnige maximale meetafstand (ondubbelzinnig bereik). Alleen een ondubbelzinnige maximale meetafstand of een ondubbelzinnige maximale snelheidsmeting kan tot een maximum worden geoptimaliseerd. Deze tegengestelde constellatie wordt ook wel het Doppler dilemma genoemd.
Indien de duur van de zendpuls veel kleiner is dan de puls-volgende periode, dan kan de relatie c0 /2·Rmax worden gebruikt voor fPRF:
| Rmax · vr < | c02 | (4) |
| 8 ftx |
De zendfrequentie ftx bepaalt dus alleen de mate waarin een unieke afstand en een unieke snelheid van doelen gelijktijdig kunnen worden gemeten.
Het Doppler-dilemma: Een lage pulsherhalingsfrequentie voor ondubbelzinnige meting van een grote afstand resulteert tegelijkertijd in een zeer slecht bereik voor ondubbelzinnige snelheidsmeting (en vice versa).
De keuze van een gunstige pulsherhalingsfrequentie is dan ofwel een compromis, ofwel moeten aanvullende maatregelen worden genomen om beide grootheden in een voldoende groot meetbereik te verkrijgen. Zo kan bijvoorbeeld een extreem hoge zendfrequentie worden gekozen of kunnen de zendimpulsen worden voorzien van een individuele modulatie, waardoor echosignalen van een vorige puls opnieuw kunnen worden toegewezen, ook al werden zij pas in een volgende pulsperiode ontvangen.

