Pulse resolution volume

Figure 1: The resolution cell
What is the radar resolution?
Pulse resolution volume
The pulse resolution volume and resolution cell characterize the joint resolving capability according to the range and angular coordinates. Usually, the pulse resolution volume is assumed to be limited by the half-power beam width φ of the antenna directivity pattern (−3 dB) and the length Δt = τi/ 2, with τi as the duration of the transmit pulse (or, in the case of intra-pulse modulation, by the duration of the signal at the output of the pulse compression device).

Figure 1: The pulse resolution volume or resolution cell
In the case of a very narrow pencil beam, i.e. with small values of the angles Θaz and Θel, the size of the pulse resolution volume can be calculated according to the following equation:
| V = R2· | c0·τ | · θaz θel | (1) |
| 2 |
The pulse resolution volume can also be considered as cylindrical depending on the used model of an approximation of the antenna pattern to simple geometric shapes. In this case, the pulse resolution volume is calculated according to:
| V = | π | ·R2· | c0·τ | · θaz θel | where | c0 = speed of light; R = distance to the radar antenna (range); τ = duration of the transmitted pulse. |
(2) |
| 4 | 2 |
In equations (1) and (2) it is assumed that the values of the angles Θaz and Θel are given in radians. If they are in degrees, they should be converted to radians by multiplying by (π/180).
The wider the spectrum of the considered transmit pulse and the narrower the antenna directivity pattern are, the smaller is the pulse resolution volume and the higher is the resolution capability of the radar station. At the same time, the interference immunity from passive disturbances distributed in space (dipole reflectors, ionized clouds, atmospheric structures, fixed targets) increases.
In weather radar, the pulse resolution volume has a greater importance. Since the pulse resolution volume increases with increasing distance, many more raindrops now fit into it for the same rain intensity: the effective reflection area will thus also increase. Therefore, the basic radar equation in weather radar has a completely different form than in an air surveillance radar.
Because of this, in weather radar we also speak of a volume target: the volume target completely fills the pulse resolution volume. In contrast, surveillance radars usually locate point targets: The reflecting object gets lost in the ever increasing pulse resolution volume with increasing distance.
Please do not confuse the pulse resolution volume with the size of a range cell in radar signal processing, i.e. the memory cell corresponding to a range segment. Such range segment should be at most half the size of the pulse resolution volume.
Radar
passive
receiver
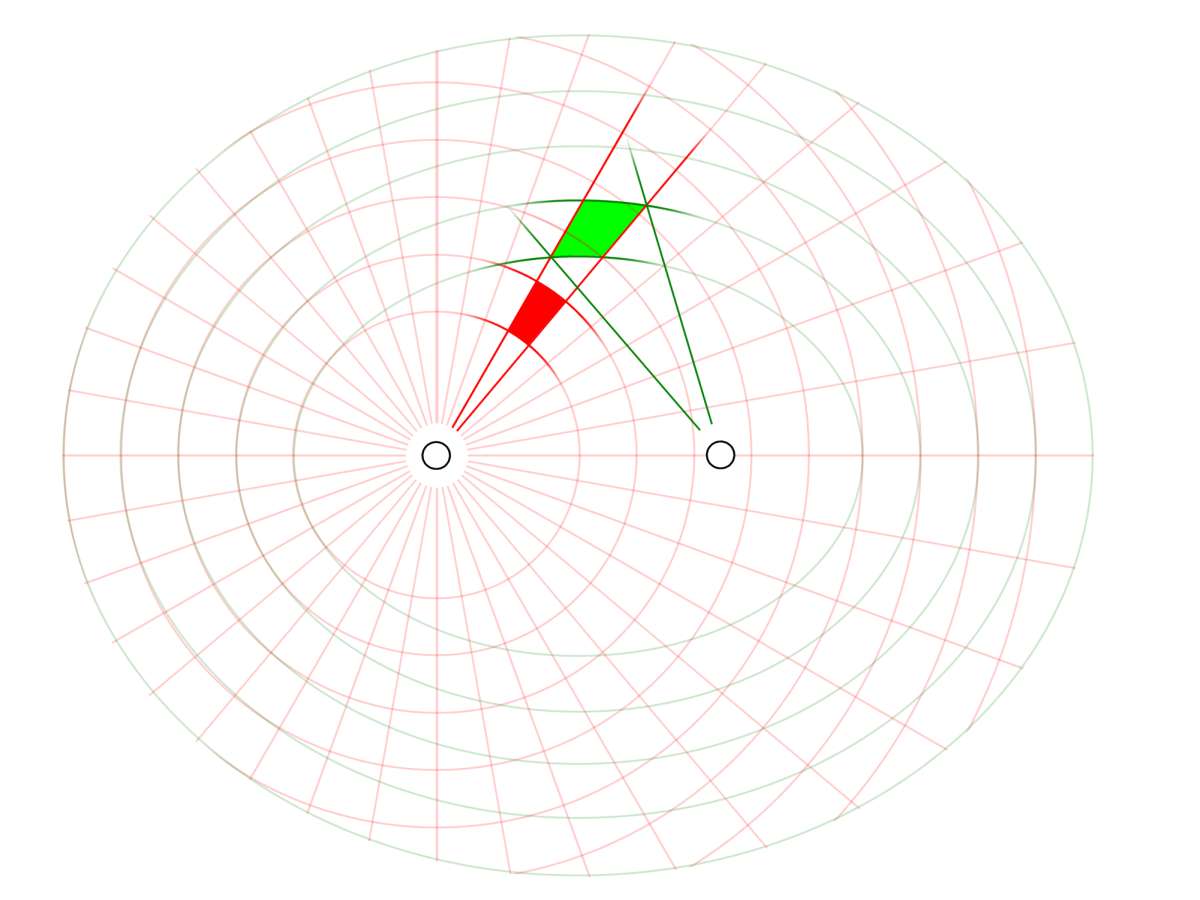
Figure 2: Comparison resolution cell of monostatic radar and bistatic radar

Radar
passive
receiver
Figure 2: Comparison resolution cell of monostatic radar and bistatic radar
Resolution cell with bistatic radar
The resolution cell with bistatic radar is spatially much more variable than with a monostatic radar. This effect is because the bistatic passive receiver does not use a directional antenna. Thus, it is fixed to the half-power beamwidth of the transmitting antenna and receives everything illuminated by the transmitter. For air surveillance radar, this has little significance. However, for weather radar, this changes the entire radar equation for volume targets since the pulse resolution volume not only changes as a function of distance but now also as a function of direction! Therefore requires in weather radar a normalization of the received echo signals to a standard size of the pulse resolution volume to make the reflectivities comparable.
The resolution should also not be confused with accuracy. Nevertheless, in most radar projects, a first guess for the accuracy figure (one standard deviation) will be half the value of the corresponding resolution. When the radar is realized, the accuracy is frequently better than the first guess because: e.g., the range accuracy is a characteristic of the measurement of the elapsed time between the departure of the transmitted pulse and the arrival of the echo at the receiver. If the transmitted pulse is a perfect rectangular one, the received pulse will look like a Gaussian curve because the receiver bandwidth is finite; in addition, the noise will disrupt the Gaussian shape of the received pulse. Hence it is obvious that the accuracy of this measurement is not really linked to the pulse width (which defines the range resolution) but rather on the receiver signal strength (which is linked to the range). Hence the range error should increase with the range.
