Winkelreflektor oder Radarreflektor


Bild 1: triangularer Winkelreflektor als Ausschnitt eines hohlen Würfels

Bild 2: Reflexion an zwei im rechten Winkel zueinander stehende Flächen
Winkelreflektoren werden verwendet, um ein besonders starkes Radarecho von Objekten zu erzeugen, die sonst nur über eine sehr geringe effektive Reflexionsfläche verfügen. Ein Winkelreflektor besteht aus zwei oder drei elektrisch leitenden Flächen, die zueinander in einem Winkel von 90° angebracht sind. Eintreffende elektromagnetische Wellen werden durch Mehrfachreflektion in genau die Richtung zurückgeworfen, aus der sie kommen. Somit ergeben auch kleine Objekte mit geringer Reflexionsfläche ein ausreichend starkes Echo.
Die Einzelflächen des Winkelreflektors sollten groß gegenüber der Wellenlänge sein. Je größer ein Winkelreflektor ist, desto mehr Energie wird reflektiert. Winkelreflektoren werden an kleineren Booten möglichst weit oben an einem Mast befestigt, um durch die Erdkrümmung verursachte Reichweitenverluste zu verringern. Dort, wo eine zu große Windlast stören würde, werden auch kugel- oder zylinderförmig verkleidete Versionen verwendet.
Wenn in den dreidimensionalen Raum zurückgestrahlt werden soll, dann muss der Winkelreflektor aus drei reflektierenden Blechen bestehen. Er wird dann trihedraler Winkelreflektor genannt. Es finden also drei Reflexionen statt, ehe der Strahl wieder in die Ursprungsrichtung zurückreflektiert wird. Mathematisch wird dieser Fall wie eine zweifache Anwendung der Formel für nur zwei reflektierende Flächen behandelt. (Das Ergebnis des ersten Durchlaufs der Formel wird als einer der beiden Eingangswerte beim zweiten Durchlauf verwendet.)
Berechnung von Winkelreflektoren
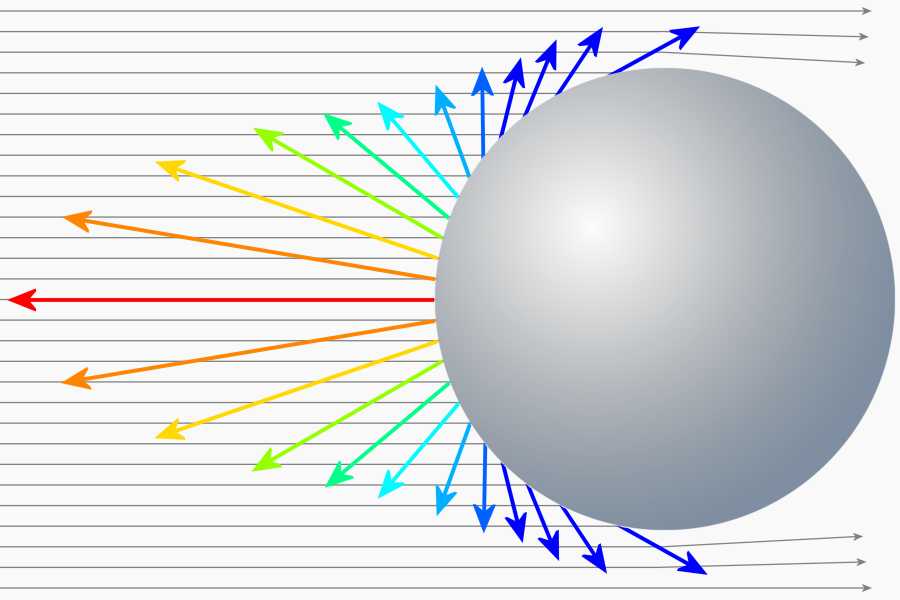
Bild 3: Die Referenz für die effektive Reflexionsfläche: eine metallische Kugel, die in der Ansicht einen (projizierten) Kreis mit einer Fläche von 1 m2 bietet.

Bild 3: Die Referenz für die effektive Reflexionsfläche: eine metallische Kugel, die in der Ansicht einen (projizierten) Kreis mit einer Fläche von 1 m2 bietet.

Bild 4: Abhängigkeit der effektiv sichtbaren Fläche vom Einstrahlwinkel des Radargerätes
Die Angabe von einer Fläche beruht auf dem Vergleich mit einem isotropen Kugelstrahler. Hier wird als Referenzreflektor ein kugelförmiger idealer Leiter angenommen, dessen Projektion auf eine Ebene senkrecht zur Projektionsrichtung (sprich: dessen Schatten auf dieser Ebene) eine Fläche von einem Quadratmeter aufweist. Diese kreisförmige Fläche hat einen Durchmesser von etwa 1,33 m. Von diesem Referenzreflektor ist jedoch nur eine sehr kleine Fläche als Rückstrahler wirksam: es sind nur wenige Zentimeter genau in der Mitte, welche die ankommende Energie in die Richtung des Radargerätes reflektieren. Alle anderen Flächen verteilen die ankommende Energie gleichmäßig im Raum. Daraus ergibt sich, dass ein kleiner handlicher Winkelreflektor mit nur wenigen Zentimetern geometrischer Ausdehnung eine effektive Reflexionsfläche von mehreren Quadratmetern haben kann. Hier muss man einfach nur wissen, dass diese Zahl von beispielsweise 12 m2 eigentlich nur aussagt, dass dieser kleine Winkelreflektor in einer bestimmten Resonanzfrequenz die gleiche wirksame Reflexionsfläche hat, wie 12 solcher Kugeln mit je einem Quadratmeter auf eine Ebene projizierter Fläche!
Eine solche Kugel würde, da sie richtungsunabhängig ist, auch bei einem bistatischen Radar ein Echosignal erzeugen. Das kann ein Winkelreflektor nicht. Die Energie, die bei einer Kugel in fast alle Richtungen verstreut wird, konzentriert der Winkelreflektor nur in genau die Richtung, von der aus er angestrahlt wird. Daraus ergeben sich für Winkelreflektoren in bestimmte Richtungen effektive Reflexionsflächen, welche die geometrischen Abmessungen des Winkelreflektors weit übersteigen.
Bei der Berechnung müssen drei Aspekte beachtet werden. Die effektive Rückstrahlfläche ist abhängig von:
- der frequenzunabhängig berechneten sichtbaren Fläche,
- dem Einstrahlwinkel des Radargerätes und
- mögliche Resonanzen bei bestimmten Frequenzen.
Sichtbare Fläche
Wenn (vorerst) davon ausgegangen wird, dass die Kantenlängen des Winkelreflektors wesentlich größer als die Wellenlänge ist, dann kann die Berechnung der effektiven Fläche nach den Gesetzen der geometrischen Optik vorgenommen werden. Die Grundlage der Berechnung ist somit eine Projektion des Winkelreflektors auf eine der Radarstrahlung lotrecht gegenüberliegenden Fläche. Im Bild 5 ist das die Strecke AB. Vorstellen kann man sich das als einen (Radar-) Schatten des Winkelreflektors auf eine gedachte senkrecht zur Radarstrahlung liegenden Ebene. Diese äqivalente (nur rechnerisch existierende) Fläche ist dann am größten, wenn die Strahlung parallel zur Symmetrieebene, also mit einem Winkel von genau 45° auf alle Platten des Winkelreflektors treffen.
Eine Ausnahmebedingung ist dann gegeben, wenn die Strahlung genau senkrecht auf eine der Teilflächen des Winkelreflektors trifft. Dann wirkt dieser mit seiner gesamten Fläche als planarer Spiegel. Deshalb ist die im Folgenden hergeleitete Formel auf die Bedingung eingegrenzt, dass die eintreffende Strahlung nur weniger als 45° von der Symmetrieebene („Boresight“) abweichen darf.
In diesem Fall ist die Länge des „Schattens“ eine Seite eines gleichschenkligen Dreiecks mit der Seitenlänge des Winkelreflektors als Hypothenuse. Die Fläche ist dann:
| Aproj = AWR· 20,5 | mit | AWR = als die Fläche nur einer Seite des Winkelreflektors Aproj = ihre Projektion, also ihr „Schatten“ |
(1) |
Aus der Tabelle auf der Seite mit der Erklärung der effektiven Rückstrahlfläche kennen wir die Formel für die Berechnung der Rückstrahlfläche einer flachen Platte. Diese ist hergeleitet aus der Berechnung der Freiraumdämpfung, die eine rechteckige Platte als einen Ausschnitt aus einer Kugeloberfläche betrachtet:
| σ = | 4·π·A2 | mit | A = Fläche einer spiegelnden Platte λ = Wellenlänge des aufklärenden Radargerätes |
(2) |
| λ2 |
Diese Formel kann allgemein dafür verwendet werden, die effektive Reflexionsfläche zu berechnen, wenn die wirksame Fläche des Winkelreflektors bekannt ist (siehe Beispiel). Die folgenden Ableitungen dieser Formel haben nur die Erweiterung, die durch Parallelprojektion entstandene Fläche Aproj mit reell messbaren Flächen oder Strecken, wie etwa eine Kantenlänge, zu ersetzen. Mit Einsatz der Formel (1) in die Formel (2) erhalten wir:
| σ = | 4·π·(AWR · 20,5)2 | = | 8·π·(AWR)2 | mit | AWR = Fläche einer Wand des Winkelreflektors λ = Wellenlänge des aufklärenden Radargerätes |
(3) |
| λ2 | λ2 |
Diese Formel gilt für zweiflächige Winkelreflektoren und wenn diese aus der Hauptrichtung („Boresight“) durch ein Radargerät angestrahlt werden. Die Angabe der Wellenlänge ist hier noch keine Resonanz, sondern ist eine Folge dessen, dass in der Herleitung der Formel zur Freiraumdämpfung ein fiktiver Antennengewinn (genauer: die Apertur der Empfangsantenne) eingeflossen ist. Seefahrer können als Wert für für die Wellenlänge pauschal 3 cm ansetzen, da die meisten maritimen Navigationsradarsysteme bei etwa 10 GHz arbeiten.

Bild 5: Die Fläche der Projektion verringert sich auf einer Seitenlänge zur Strecke AC
Einstrahlwinkel
Für die von dem Winkel von 45° abweichend auf diese Platte eintreffenden Strahlen sind die „Schatten“ der einzelnen Seiten nicht mehr gleich groß. Effektiv wirkt aber nur die kleinere Projektionsfläche des Winkelreflektors. Denn selbst wenn die zweite Fläche des Winkelreflektors einen viel größeren „Schatten“ werfen würde, kann sie doch nur die Energie erneut spiegeln, die auch von der ersten, kleiner projizierten Platte gespiegelt wird. Die auf die Fläche mit der einen Seite BC treffende Energie wird nur einmal gespiegelt und somit in einen anderen Winkel abgestrahlt. Also in eine Richtung, die nicht den Empfänger des Radargerätes erreicht und deswegen durch das monostatische Radar nicht nutzbar ist. Die effektiv nutzbare Fläche ist also nur doppelt so groß, wie die kleinere Projektionsfläche. Für Winkel 0° < Θ < 90° betragen die effektiven Abmessungen der Projektion:
| Aäquiv = kleinere Teilfläche + Teil der größeren Teilfläche | (4) |
| Aäquiv = AWR·sin Θ + AWR·tan Θ ·cos Θ = 2 AWR·sin Θ |
| σ = | 16·π·(AWR)2 | ·sin2 Θ | (5) |
| λ2 |
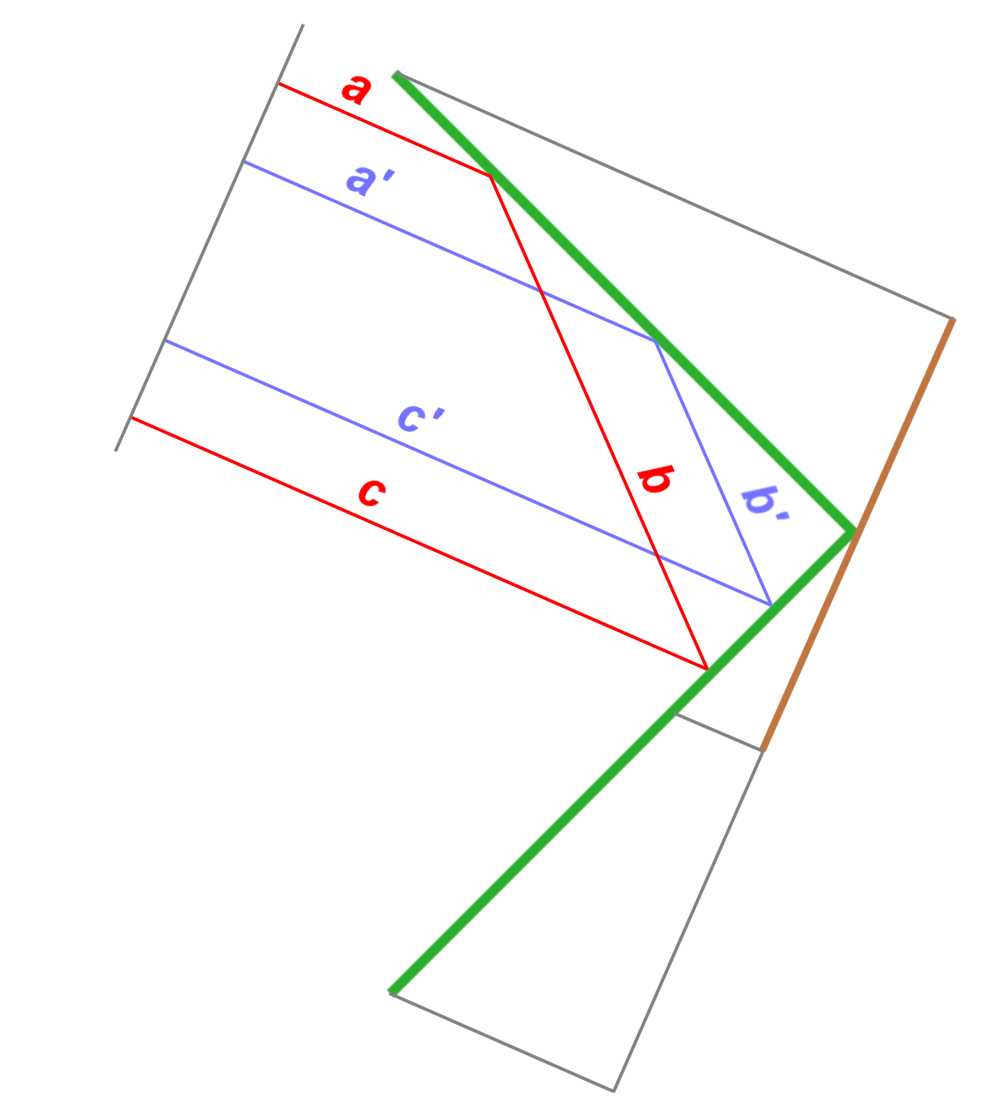
Bild 6: Gleiche Phasenlage wegen gleicher Strecken: a+b+c = a'+b'+c'
Einfluss der Resonanz
Die Vorstellung, dass die Metallfläche für elektromagnetische Wellen wie ein Spiegel funktionieren, ist nur eine Vereinfachung. Eigentlich nimmt die Metallfläche die Energie auf, schwingt somit selber und strahlt die Energie wieder ab. Die Richtwirkung wird durch die Phasenunterschiede der am jeweiligen Ort stattfindenden Schwingungen bewirkt, die durch die Laufzeitunterschiede des aus schrägem Winkel eintreffenden Strahlungsfeldes entstanden sind. Die Ströme, die in einer einfachen Metallplatte durch dieses Feld induziert werden, erzeugen im Empfänger ein äußerst schwaches Signal, weil viele Nebenkeulen die Energie der Sekundärstrahlung verteilen. Erst wenn sich diese beiden Metallplatten im Winkel von 90° gegenüberstehen, dann erzeugen die Ströme ein intensiveres Feld der Sekundärstrahlung, die nur in die Einfallsrichtung der Strahlung phasengleich sind.
Ähnlich wie bei einem Düppel kann nun die Größe der reflektierenden Fläche eine Resonanz mit der Wellenlänge erhalten. Die reflektierende Fläche muss in der Polarisationsrichtung mindestens die halbe Wellenlänge betragen. Aber! Es sind mindestens zwei reflektierende Flächen beteiligt, also beträgt die kleinste Resonanzlänge des Winkelreflektors eine ganze Wellenlänge.
Durch die Resonanz kann bei der Breite des Winkelreflektors von Lambda eine bis zu vierfache effektive Reflexionsfläche gemessen werden, als es die geometrischen Ausmaße vermuten lassen. Der Reflektor kann auch mit Oberwellen angeregt werden. Der Gewinn durch die Resonanz verringert sich aber mit jeder höheren Oberwelle um die Hälfte. Ab der zehnfachen Wellenlänge ist kein Einfluss mehr zu beobachten. Eine negative Auswirkung hat das Resonanzverhalten aber ebenfalls: bei ungeradzahligen Vielfachen von der halben Wellenlänge (1,5λ, 2,5λ …) ist eine Verringerung der effektiven Reflexionsfläche um die gleichen Faktoren zu beobachten.
Trihedrale Winkelreflektoren

Bild 7: Winkelreflektor aus drei quadratischen Flächen

Bild 7: Winkelreflektor aus drei quadratischen Flächen
Da der zweiflächige (dihedrale) Winkelreflektor bei einer Abweichung der einfallenden Strahlen von der normal zur Kante stehenden Ebene nicht mehr in Richtung des Radargerätes zurückstrahlt, werden meist dreiflächige Winkelreflektoren benutzt. Diese werden in der Geometrie als trihedral bezeichnet.
Trihedraler Winkelreflektor aus quadratischen Blechen
Diese Winkelreflektoren bestehen aus drei quadratischen Blechen, die im Winkel von 90° miteinander verschweißt sind. Die projizierte Fläche besteht also nun aus drei Teilflächen, die aber ebenso mit der Formel (1) berechnet werden. Nur muss diese Formel jetzt pro Fläche zweimal angewendet werden, dafür geht das Ergebnis dreifach ein.
| σ = | 12·π·(AWR)2 | ·sin2 Θ | (6) |
| λ2 |
Auch diese Formel gilt nur für dreiflächige Winkelreflektoren und wenn diese aus der Richtung der Symmetrieachse („Boresight“) durch ein Radargerät angestrahlt werden. Es ist also der Maximalwert, der erreicht werden kann. Praktisch wird der Winkelreflektor aber in den meisten Fällen wesentlich weniger effektive Reflexionsfläche zeigen, da dieser hier berechnete Sonderfall sehr selten eintritt.

Bild 8: Winkelreflektor aus drei dreieckigen Flächen

Bild 8: Winkelreflektor aus drei dreieckigen Flächen
Trihedraler, triangularer Winkelreflektor (aus dreieckigen Blechen)
Ein Winkelreflektor mit drei quadratischen Flächen ist mechanisch relativ unstabil. Meist wird deswegen die Teilfläche (wie in Bild 1 und Bild 8 gezeigt) auf dreieckige Flächen reduziert. Damit reduziert sich auch die effektive Rückstrahlfläche wesentlich. Dafür hat ein Winkelreflektor aus dreieckigen Flächen einen größeren Öffnungswinkel. Die effektive Rückstrahlfläche wird für diesen triangularen Winkelreflektor berechnet nach:
| σ = | 4·π·a4 | mit | a = Länge der Seitenkanten der drei gleichschenkligen Dreiecke λ = Wellenlänge des aufklärenden Radargerätes |
(7) |
| 3·λ2 |
Ein solcher Winkelreflektor hat einen Öffnungswinkel von fast 40°, bevor die reflektierte Energie unter die vom Antennendiagramm bekannten −3dB- Grenzen abfällt. Deshalb werden bis zu acht solcher Winkelreflektoren zu einem Würfel zusammengesetzt. Nun wird in jede Richtung mindestens ein Reflektor wirksam.
Dieser Winkelreflektor besteht zeichnerisch aus 12 gleichschenkligen Dreiecken. Beim praktischen Bau geht man aber unter Vernachlässigung der Blechdicke von drei gleich großen quadratischen Blechen aus, von denen eines diagonal halbiert und ein zweites diagonal geviertelt wird. Der Winkelreflektor wird dann aus diesen sieben Teilen symmetrisch zusammengeschweißt (in der Mitte und am Rand gepunktet genügt: aber ganz wichtig: auf rechte Winkel achten!). Bei einer Kantenlänge der quadratischen Bleche von 0,5 m hat dann dieser Eigenbau-Winkelreflektor im I/J-Band eine effektive Rückstrahlfläche von weit mehr als dem fünfhundertfachen Wert, den ein kleines Ruderboot ohne diesen Winkelreflektor hätte. Das ist dann ein in der Binnenschifffahrt nicht mehr zu übersehendes Zielzeichen auf dem Radar!




