Направленность и усиление антенны
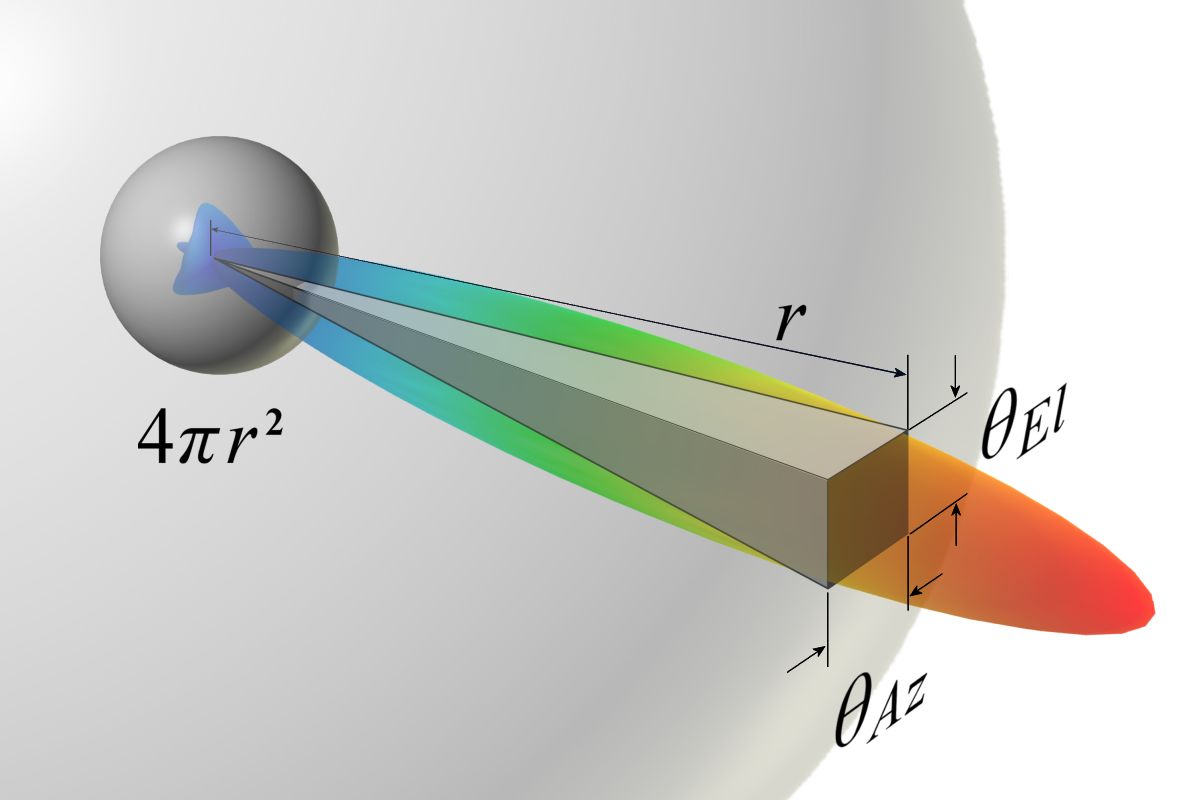
Рисунок 1. К сравнению поверхности, облучаемой направленной антенной, и сферической поверхности.
(Обратите внимание: при сравнении радиус сферы должен быть равен расстоянию до прямоугольника от центральной точки.)

Рисунок 1. К сравнению поверхности, облучаемой направленной антенной, и сферической поверхности.
(Обратите внимание: при сравнении радиус сферы должен быть равен расстоянию до прямоугольника от центральной точки.)
Направленность и усиление антенны
Коэффициент усиления антенны G объединяет коэффициент направленного действия D и эффективность η антенны в один простой для использования параметр.
Коэффициент направленного действия антенны
Коэффициент направленно действия антенны определяется как отношение плотности мощности S (интенсивность излучения на единицу площади) реальной антенны в ее основном направлении к аналогичной величине для гипотетической, не существующей в действительности, изотропной антенны, излучающей равномерно во всех направлениях. Таким образом, плотность мощности изотропного излучателя равномерно распределяется по поверхности сферы. Реальная же антенна имеет более или менее выраженную направленность излучения, которая количественно характеризуется значением коэффициента направленного действия. С учетом приведенного выше, формула для его определения выглядит так:
| D = | S | где |
S – плотность мощности реальной антенны в основном направлении ее излучения; Si – плотность мощности изотропного излучателя. |
(1) |
| Si |
Направленная антенна концентрирует излучаемую ею мощность только на небольшой части поверхности сферы. Величина этой части может быть определена в относительных единицах по отношению ко всей площади сферы. Площадь этой части может также быть определена на основании значений ширины луча антенны (в радианах) по уровню половинной мощности. (Очевидно, что в формуле для площали участка поверхности используются линейные размеры этого участка. Они определяются как произведение угловых размеров участка на радиус сферы. При вычислении отношения площадей радиус, входящий и в числитель и в знаменатель, сокращается). Линейные размеры искомой эффективной площади определяются в кратности к длине волны.
| D = | Aсферы | ≅ | 4π r2 | = | 4π | = | 4π · Aэфф | где |
Aсферы – площадь поверхности сферы единичного радиуса; Aэфф = b·h – эффективная апертура на поверхности сферы; θAz – ширина луча по уровню половинной мощности (в радианах) в горизонтальной плоскости; θEl – ширина луча по уровню половинной мощности (в радианах) в угломестной плоскости; b – ширина участка поверхности; h – высота участка поверхности. |
(2) |
| Aэфф | θAz · θEl | λ/b · λ/h | λ2 |
(Здесь, однако, присутствует неточность, поскольку поверхность Aэфф = b·h представляет собой плоскую поверхность, а не сферическую. Соответствующая погрешность будет тем меньше, чем меньше площадь b·h по сравнению с площадью сферы, то есть, чем выше направленность антенны. Этой погрешностью можно пренебрегать при ширине луча по уровню половинной мощности до 20°).
Коэффициент усиления антенны
Коэффициент направленного действия антенны является существенным составлящим коэффициента усиления антенны. Однако, кроме него, при анализе реальных антенн должны учитываться и потери. Излучаемая антенной мощность пропорциональна поступающей от передатчика мощности, которая может быть легко измерена на фидере антенны. Однако часть подводимой от передатчика мощности теряется в антенне на питающей линии за счет ее омического сопротивления. Эти потери и определяют эффективность антенны. Для идеальной антенны без потерь коэффициент усиления был бы равен коэффициенту направленного действия. Для реальных антенн коэффициент усиления всегда меньше коэффициента направленного действия:
| G = η· D | (3) |
Коэффициент усиления антенны не всегда должен быть больше 1. Существуют также антенны с коэффициентом усиления меньше 1. Обычно это антенны для измерений, где важно достичь равномерности коэффициента усиления в очень широкой полосе частот для сравнения результатов измерений в различных частотных диапазонах.
Допущения
Необходимо сделать некоторые упрощения для того, чтобы соотнести сферическую поверхность изотропного излучателя с эффективной апертурой антенны:
- Предполагается, что вся излучаемая энергия сосредоточена в основном лепестке диаграммы направленности антенны. В этом предположении боковые лепестки будут отсутствовать.
- Предполагается, что вся излучаемая антенной энергия сосредоточена в пределах измеренной ширины луча по уровню половинной мощности. Соответственно, за пределами луча излучение энергии отсутствует.
- В пределах ширины луча по уровню половинной мощности энергия распределена равномерно. (Таким образом, как правило конусообразное тело становится пирамидальным. Прямоугольник в основании полученной пирамиды имеет площадь, равную произведению ширины луча в угломестной плоскости и ширины луча в азимутальной плоскости!).
Только при перечисленных допущениях можно сравнить две упомянутые выше геометрические поверхности – прямоугольник и фрагмент сферической поверхности.
