Bistatik Radarla Koordinat Belirleme
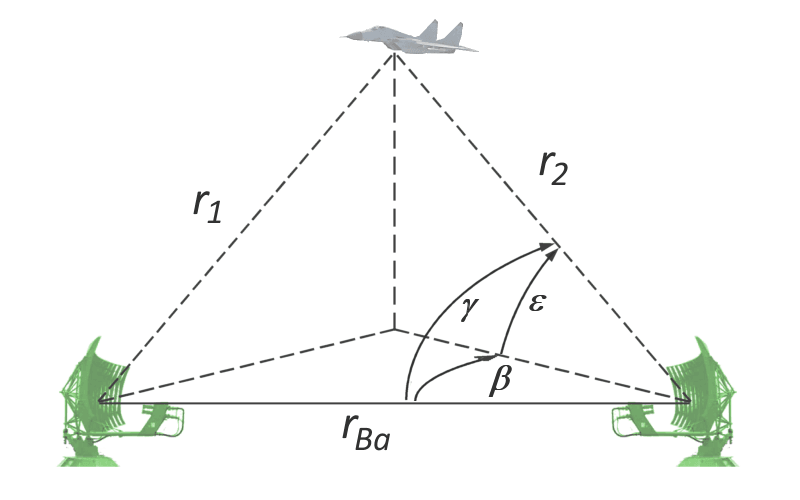
Resim 1: Bir bistatik radarla koordinat tayini
Bistatik Radarla Koordinat Belirleme
İletilen darbe alıcıya iki şekilde ulaşır: doğrudan ve hedeften yansıdıktan sonra. Toplam rΣ = r1 + r2 mesafesi ölçülür ve alınan işaretin azimut açısı β ve yükseklik açısı ε belirlenir.
rΣ mesafesini ölçmek için gerekli zaman ölçümünün başlangıcına ilişkin bilgi, iletilen darbenin kesin olarak bilinen bir rBa mesafesinin (göz önünde bulundurulan üçgenin tabanı) doğrudan alınmasıyla elde edilebilir.
rΣ mesafesi, gönderici- ve alıcı antenlerin bulunduğu odak noktalarında, hedefin bir dönüş elipsoidinin yüzeyindeki konumunu belirler.
Hedef, bu dönüş elipsoidinin yüzeyinin, yansıyan işaretin geldiği yönü karakterize eden düz çizgi ile kesiştiği noktada bulunur. Hedefin alıcı antenden r2 uzaklığı kosinüs kuralı ve ölçülen toplam mesafe rΣ kullanılarak belirlenebilir:
.print.png)
.png)
(1)
İki bilinmeyenli bu denklem sistemi aşağıdaki denkleme dönüştürülebilir:
.print.png)
.png)
(2)
γ açısının boyutu, bu üç açı arasındaki ilişkiye dayalı olarak ölçülen β ve ε açılarıyla belirlenir:
.print.png)
(3)
Yalnızca iki boyutu ölçen bir radar için γ = β.

Resim 2: Klein Heidelberg Parasit pasif radarının ölçüm prensibi
Bu prensibin ilk kullanımlarından biri İkinci Dünya Savaşı'nda Klein Heidelberg Parasit pasif radarıyla gerçekleşti. Bu radar, İngiliz Chain Home göndericilerinden gelen yayınlarını kullandı. Chain Home'un çeşitli gönderim kuleleri belirli bir programa göre çalışıyordu. Kanallardan biri bir zamanlayıcı ve bir kapı devresi (gate circuit) kullanılarak seçilebiliyordu.
Mesafe farkı, doğrudan alınan işaret ile yansıyan işaret arasındaki gecikme süresi ölçülerek belirleniyordu. İki denklemli ve üç bilinmeyenli denklem sistemindeki belirsizlik nedeniyle gecikme süresi, tüm olası konumların ortaya çıkmasına neden olur ve bu konumlar, gönderici ve alıcının odak noktasında olduğu bir elips oluşturur.
Bununla birlikte, alıcı anten döndürülebilir ve üçüncü bir değişken olarak β açısını belirlemek için anten çizgesi kullanabilir. Bu nedenle ölçüm sonucu kesindi. Doğruluk, yönler için anten modelinin ilk sıfırı kullanılarak geliştirilebiliyordu.


