Stubs

Figure 1: Current and voltage characteristics on transmission lines>

Figure 1: Current and voltage characteristics on transmission lines
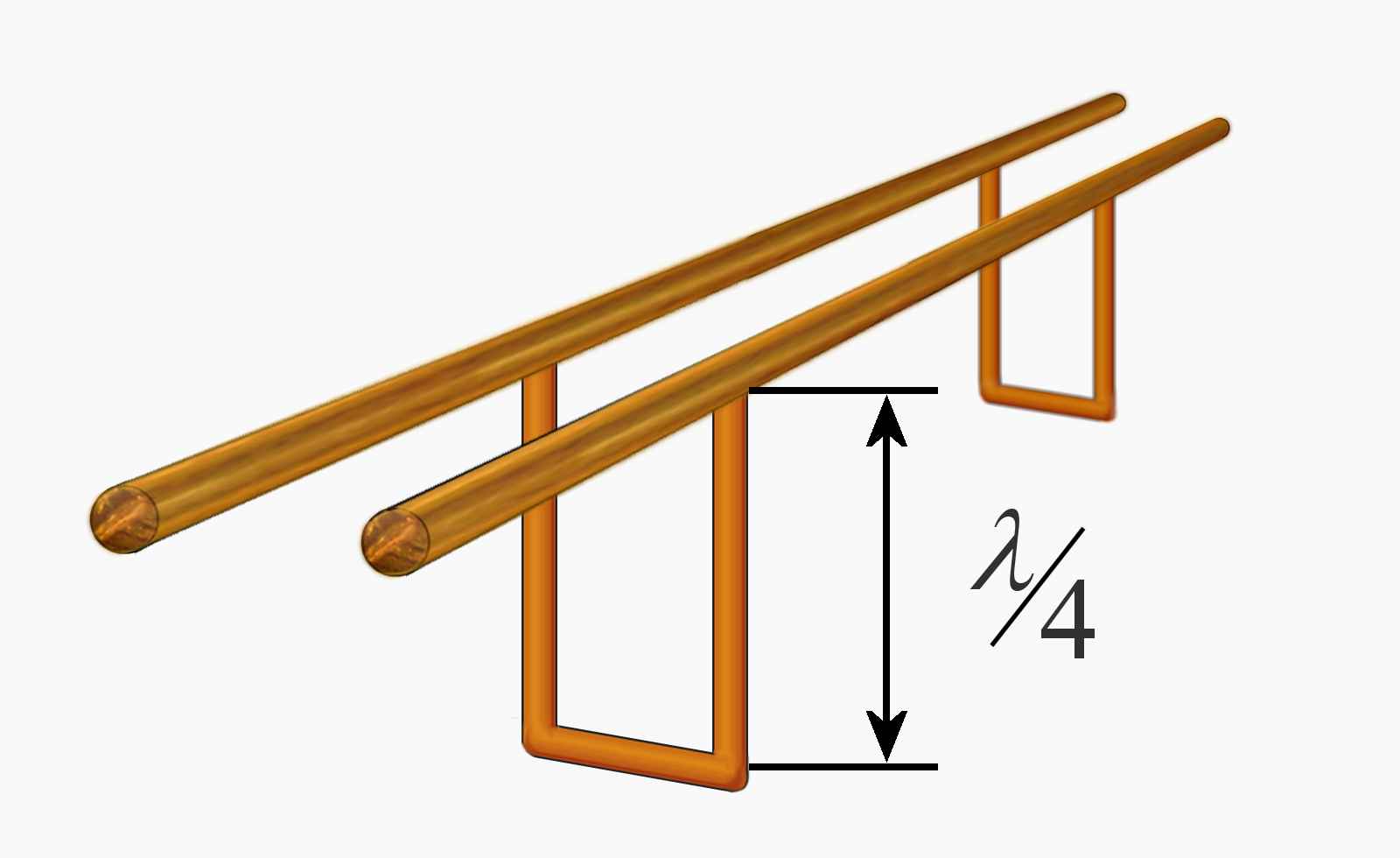
Figure 2: Stubs as spacers
Stubs
In high-frequency technology, cable sections are usually used for tuning purposes that are matched in length. Such line sections can be connected parallel to the line and are then referred to as stubs or resonant stubs. The length adjustment is an adaptation to the wavelength to be transmitted.
These line sections are deliberately mismatched: that is, they are not terminated with a resistor the size of the line impedance but are either short-circuited or left open.
A short circuit means that at this point the resistance is close to or equal to zero, so the voltage measurable at this point is also equal to zero but a maximum current flows. With an open line, no current can flow but the voltage has its maximum value at this point. With a high-frequency wave on this line, the wave is completely reflected at such mismatched points. Interference between the incoming and outgoing waves results in a standing wave. Along the line, this maximum (or in the case of a short circuit: minimum) voltage can now be repeatedly measured at a distance of half the wavelength from this mismatch.
If the distance is only a quarter of the wavelength, the ratio is reversed. The maximum voltage at the mismatch (open wire) is zero at this point, the current is maximum. If the mismatch is a short circuit, then the current is zero at this distance but the voltage is maximum.
According to Ohm’s law R = U / I, a resistance can be calculated from both values. If the voltage is zero, then the resistance is also zero; if the current is zero, then we have a division by zero: the resistance goes to infinity. For example, the lengthwise tuned line has now reversed the short circuit into its opposite: transformed it into an open line.
Applications
- Such line sections can be used as part of filters that prefer certain frequencies: those to which the calculated relationship of the length of the line section to the wavelength applies exactly. For example, in the length ¾ λ after a short circuit, they have a very high resistance and have little effect on the signal. For adjacent frequencies, however, the same length can mean ½ λ. Such frequencies are then strongly attenuated on this line.
- Two-wire lines must have a certain distance between the wires for the impedance to be correct. If such spacers are placed directly between the wires, they must be well insulated so as not to attenuate the signal. If a stub line is used instead (as shown in Figure 2), they transform the short-circuit at the lower end into a connection with an almost infinite resistance - i.e. with very good insulation.

