Winkelauflösungsvermögen

Bild 1: Der Abstand SA ist entfernungsabhängig
Was ist Winkelauflösungsvermögen?
Winkelauflösungsvermögen
Das Auflösungsvermögen im Seitenwinkel oder die Azimuthauflösung gibt bei Zielen mit gleicher Entfernung zur Antenne an, welchen Mindestabstand die Ziele tangential zueinander haben müssen, damit sie durch das Radar unterschieden und als zwei verschiedene Zielzeichen dargestellt werden können. Im Gegensatz zur Entfernungsauflösung ist das Auflösungsvermögen im Seitenwinkel zusätzlich noch entfernungsabhängig, und zwar proportional zur Entfernung.
« Winkelauflösungsvermögen »

Bild 1: Der Abstand SA ist entfernungsabhängig
Winkelauflösung als Antennenparameter
Grundsätzlich gilt, dass bei Zielen mit gleichem Abstand zur Antenne keine Zieltrennung erfolgt, wenn beide Ziele gleichzeitig von der Hauptkeule des Antennendiagramms erfasst werden. Das Winkelauflösungsvermögen kann als reiner Seitenwinkel angegeben werden. Das ist dann der Fall, wenn eine Entfernungsangabe zu diesem Auflösungsvermögen entweder nicht sinnvoll (z.B. bei allgemeinen Beschreibungen der technischen Daten eines Radars) oder nicht möglich ist (zum Beispiel beim CW-radar).
Wenn auf einem A-Scope ein Zielzeichen als sehr großer Impuls erscheint, so kann nicht ohne Weiteres unterschieden werden, ob es das Zielzeichen von nur einem sehr großen Ziel, oder ob es zwei Zielzeichen von dicht nebeneinander fliegenden Zielen sind, deren Amplituden sich überlagern. Der Abstand zwischen den Zielen muss erst so groß werden, dass zwischen den Amplituden der beiden Ziele ein Minimum erkennbar wird.
Maßgebend für das Winkelauflösungsvermögen für ein Radar ist der Öffnungswinkel oder die Halbwertsbreite Θ der Antenne. Der formelmäßige Zusammenhang zwischen dem Öffnungswinkel und dem Auflösungsvermögen lässt sich gemäß der Winkelfunktion wie folgt darstellen:
.print.png)
.png)
(1)
- Θ = Öffnungswinkel der Hauptkeule (Theta)
- SA = Azimuthauflösung
- R = Schrägentfernung Ziel - Antenne [m]
Die Azimuthauflösung an einem analogen PPI Sichtgerät ist in der Praxis eher abhängig davon, ob der Bediener erkennt, dass in dem Zielzeichen zwei Flugzeuge enthalten sind. Systeme mit digitaler Zielerkennung können die Azimuthauflösung verbessern, weil sie die einzelnen Zielamplituden miteinander vergleichen.
Bei 3D-Radargeräten kann auch ein Auflösungsvermögen im Höhenwinkel gemessen werden. Hier ist das gleiche Verfahren wie bei der Azimuthauflösung anwendbar, als Θ wird dann der vertikale Öffnungswinkel verwendet.

Bild 2: Halbwertsbreite vs. Nullwertswinkel
(halbe Nullwertsbreite)

Bild 2: Halbwertsbreite vs. Nullwertwinkel
(halbe Nullwertbreite)
Winkelauflösung Lidar
In bestimmten Fällen (zum Beispiel bei Lidar) ist es einfacher, das Auflösungsvermögen nicht über den Weg der Halbwertsbreite zu bestimmen. Das Auflösungsvermögen eines optischen Systems ist gemäß Rayleigh definiert durch den Winkelabstand zweier gleichartiger punktförmiger Objekte bei dem das Hauptmaximum der Abbildung des einen punktförmigen Objektes in das erste Minimum der Abbildung des anderen Objektes fällt. (Beachte: Rayleigh geht davon aus, dass beide Objekte ungefähr gleich stark aktiv leuchten, wobei es egal ist, ob nun durch innere energetische Vorgänge oder ob sie beide durch eine andere Lichtquelle gleichmäßig angestrahlt werden und dessen Licht reflektieren.)
Die Definition auf Radar bezogen heißt: Das Seitenwinkelauflösungsvermögen eines Radars ist definiert als der Winkelabstand des ersten Minimums des Antennendiagramms vom Maximum der Hauptkeule (Nullwertwinkel oder halbe Nullwertbreite). In Bild 2 wird ein Antennendiagramm gezeigt, welches ein zweites Mal um genau dieses Rayleigh-Kriterium verschoben dargestellt wird. Der Nullwertwinkel ist annähernd gleich dem Öffnungswinkel der Antenne.
Um die Breite der Hauptkeule zu berechnen kann folgende Beziehung genutzt werden:
.print.png)
.png)
(1)
- λ = Wellenlänge im freien Raum
- D = Längenausdehnung der Apertur
- K = Strahlbreitenfaktor
Unter der Voraussetzung einer linearen Phasenverteilung hat jedes Amplitudenverhältnis einen entsprechenden Strahlbreitenfaktor mit der Maßeinheit Radiant (Bogenmaß). Der Strahlbreitenfaktor für die Halbwertsbreite hängt von der Art der Antenne ab und variiert zwischen 0,98 rad (≙ 56°) (für eine ideale Reflektorantenne) und 2 rad (≙ 114°). Für den Nullwinkel einer Antenne mit synthetischer Apertur beträgt der Strahlbreitenfaktor 1,22 rad (≙ 70°).
Der Nullwertwinkel bezieht sich also nur auf die halbe Breite der Hauptkeule, die Nullwertbreite und die Halbwertsbreite auf beide Hälften (siehe Bild 2). Beide Winkel (Nullwertwinkel und Halbwertsbreite) sind damit zwar ähnlich groß, aber nicht gleich. Der Größenunterschied kann aber in der Praxis näherungsweise vernachlässigt werden, man muss bei der Anwendung der Formel (1) jedoch den Bezug beachten, ob der verwendete Winkel nur die halbe Breite der Hauptkeule betrifft, oder beide Hälften.
Cross Range Resolution
Mit dem Aufkommen des Radars mit synthetischer Apertur (SAR) wurden auch dort geprägte Begriffe für andere Radarverfahren übernommen, obwohl das geometrisch andere Beziehungen sind. Eine Entfernung wird beim SAR rechtwinklig zur Bewegungsrichtung der Radarplattform gemessen. Das Auflösungsvermögen in der Bewegungsrichtung ist somit wieder rechtwinklig zur Schrägentfernung und wird hier deshalb Cross Range Resolution genannt. Die Übernahme dieses Begriffes für ein Radar mit realer Apertur ist kritisch zu sehen, denn bei einer realen Apertur ist der Abstand zwischen den Zielen nicht rechtwinklig zum Radius, sondern für jedes einzelne Ziel tangential: Der Abstand zwischen den Zielen ist dann in dem Kreis mit dem Radius R eine Sehne (siehe Bild 1).
Durch die rechnerische Nachbearbeitung hat bei SAR das Auflösungsvermögen völlig andere Zusammenhänge als bei einem Radar mit einer realen Antenne. Im Gegensatz zur realen Apertur verbessert sich die Cross Range Resolution mit der Vergrößerung der Halbwertsbreite der realen Antenne. Es können schließlich nur Echosignale von demjenigen Objekt weiterverarbeitet werden, das durch die Antenne bei einem Vorbeiflug auch in allen Messungen erfasst wird. Das sind um so mehr Messergebnisse, je größer der Öffnungswinkel der realen Antenne ist. Um so mehr einzelne Echosignale in die Verarbeitung einfließen, desto besser wird das Winkelauflösungsvermögen. Dadurch wird das Winkelauflösungsvermögen in einer größeren Entfernung besser als im Nahbereich, da der sogenannte „Fußabdruck“ des Radars mit der Entfernung sich vergrößert. Die Vergrößerung der synthetischen Apertur wirkt dem sich mit zunehmender Entfernung schlechteren entfernungsmäßigen Auflösungsvermögen entgegen. Im Gegensatz zur realen Apertur ist deshalb die Cross Range Resolution beim SAR etwa konstant auch mit zunehmender Entfernung.
Seitenwinkelauflösung mit CW-Radar

Bild 3: Einfluss des Abstandes auf die Seitenwinkelauflösung
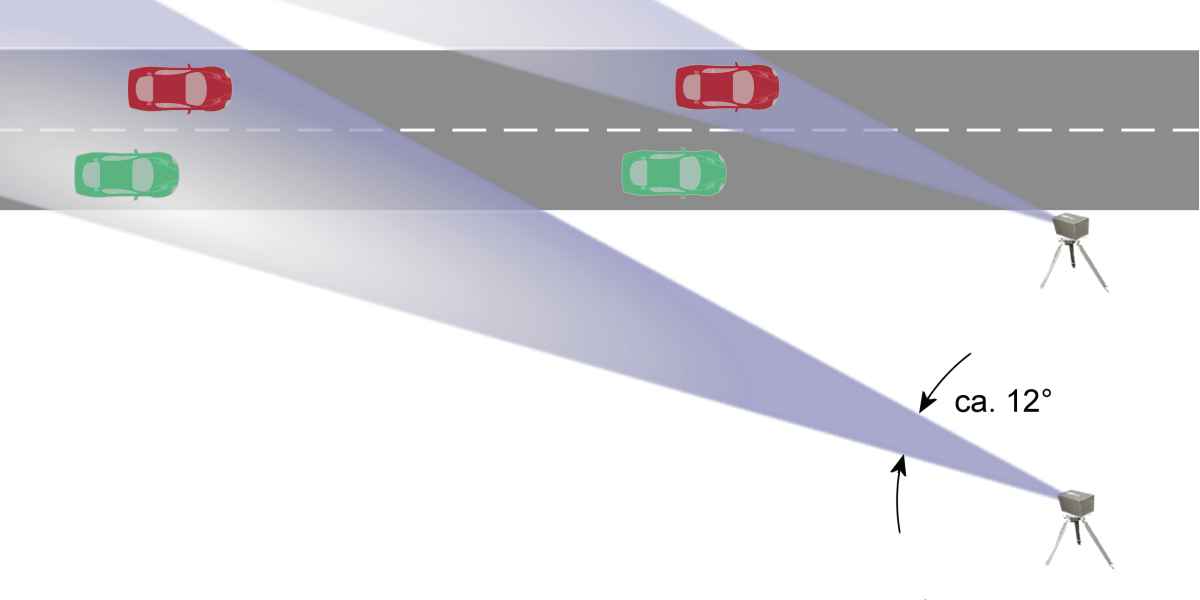
Bild 3: Einfluss des Abstandes auf die Seitenwinkelauflösung
Auf kurze Entfernungen sind mit einem CW-Radar extreme Genauigkeiten mit geringem Aufwand möglich. Daher werden solche Radargeräte gern genutzt, um zum Beispiel im Straßenverkehr Geschwindigkeiten zu kontrollieren. Die Winkelauflösung wird nach Gleichung (1) ausschließlich durch die Halbwertsbreite Θ der Antenne und deren Abstand R zum Messobjekt bestimmt.
Ein Problem bei Radargeräten ist, die gemessenen Werte einem gegebenen reflektierenden Objekt auch eindeutig zuzuordnen. Bei einem CW-Radar ist eine Trennung von zwei gleichzeitig reflektierenden Objekten oft nicht möglich. Selbst wenn es möglich ist, dann kann nicht gesagt werden, welches Objekt die größere und welches Objekt die kleinere Geschwindigkeit hatte. Ist der Abstand zum Messobjekt groß, dann verbreitert sich das Antennendiagramm und verschlechtert die Winkelauflösung. In diesem Fall muss dann die Messung verworfen werden. Es dürfen auf dem Beweisfoto nicht zwei Fahrzeuge zu sehen sein, da nicht nachweisbar ist, welches Fahrzeug zu schnell war. Somit ist hier das Auflösungsvermögen eher von der Nullwertsbreite der Radarantenne abhängig, wobei allerdings auch ein Empfang mittels der Nebenkeulen möglich ist. Bei diesem Einsatz kann durch möglichst geringem Abstand zum Straßenrand mögliche Messergebnisse verbessert werden. Manchmal verläuft zwischen Fahrbahn und Messaufbau noch ein Radweg und erzwingt so einen größeren Abstand. Dann sind Messungen nur möglich, wenn die Verkehrsdichte gering genug ist.
Ausnahmen
Die grundsätzliche Feststellung, dass bei Zielen mit gleichem Abstand zur Antenne keine Zieltrennung erfolgt wenn beide Ziele gleichzeitig von der Hauptkeule des Antennendiagramms erfasst werden, gilt eigentlich nur für klassische Radargeräte. Deshalb wird oft die Formulierung gewählt, dass wenn die Ziele einen seitlichen Abstand von der Größe der Hauptkeule haben (hier wird meist die durch den Hersteller der Antenne angegebene Halbwertsbreite zugrunde gelegt) eine Zieltrennung leichter fallen würde. Diese Formulierung suggeriert, dass manchmal auch innerhalb der Hauptkeule zwei Ziele voneinander getrennt werden könnten.
Das ist tatsächlich der Fall, wenn eine Zielidentifizierung durch eine Untersuchung des Doppler-Spektrums und dem Vergleich mit in Datenbanken gespeicherten Signaturen durchgeführt wird. So kann unter Umständen festgestellt werden, dass innerhalb eines Echoimpulses zwei verschiedene bekannte Radarsignaturen enthalten sind. Das resultiert aus der Unmöglichkeit, dass die Drehzahl der Turbine eines Flugzeuges mit der des zweiten Flugzeuges synchron sein kann. Die Dopplerfrequenzen der Reflexionen der Turbinenschaufeln (die sogenannte Jet Engine Modulation, JEM) unterscheiden sich und lassen so den Schluss zu, wie viele Flugzeuge an diesem Echosignal mitgewirkt haben.
Referenz:
- IEEE, ”IEEE Standard Radar Definitions,“ Radar Systems Panel, IEEE Aerospace and Electronics Systems Society, Report No. IEEE Std 686-2008, 2008.
